Fraktallar Geometriyasi: Jozibador Va Beto‘xtov Olam To'liq Malumot Oling

Fraktallar geometriyasi: jozibador va beto‘xtov olam to’liq malumot oling

Bir necha asrlar mobaynida matematika Yevklid geometriyasining ajoyib olamiga maftun boʻlib yashadi. Lekin bugungi zamon matematikasi oʻziga boshqa bir yoʻnalish — fraktallar geometriyasini kashf qilgan. Fraktallar geometriyasi bizning qarshimizda borliqning butunlay yangi jozibasini ochib bermoqdaki, hayratlanmaslikning iloji yoʻq.

Tasavvur qiling, biz Oʻzbekistonning Turkmaniston bilan chegarasi uzunligini xaritaga qarab aniqlamoqchimiz. Buning uchun chegara chizigʻi boʻylab ikki nuqta orasidagi masofani oddiy chizgʻich bilan oʻlchab, olingan natijani xaritaning miqyos-masshtabi bilan taqqoslab, chegaraning umumiy uzunligini topishimiz mumkin boʻladi.

Natijada chegara uzunligining taxminiy, taqriban yaqin qiymatiga ega boʻlamiz. Albatta, bu asl real chegara uzunligining eng aniq oʻlchanishi yoki hisoblanishi boʻla olmaydi. Bu masofani aniqlashning yana bir usuli — sirkul olib, uning ignalari oraliq masofasini 1 sm qilib aniq belgilab qotirib, xarita boʻylab chegarani boshidan oxirigacha qadamlab oʻlchab chiqish.

Bunda oxirida sirkulning barcha qadamlari soni yigʻindisi chiqariladi va bu orqali chegaraning umumiy uzunligini hisoblash mumkin boʻladi. Bu usul bilan olingan natija avvalgisidan koʻra aniqroq boʻladi. Lekin chegara tep-tekis toʻgʻri chiziq boʻlmagani sababli sirkulni har safar burib, yangi nuqtaga yoʻnalish olayotganimizda chegaraning hamma qismini ham qamrab ololmasligimizni tushunib boramiz.

Agar xarita batafsilroq yoritilgan boʻlsa, unda sirkul qadami oʻlchamini biroz kichraytirib turib, notekis chiziqli, burama-egri chiziqli chegara chiziqlarini ham qamrab olgan holda yanada aniqroq natijaga ega boʻlish mumkin. Hatto bir mamlakat hududining ikkinchisi ichkarisiga turtib kirgan kichik yer uchastkasi chegarasini ham aniq oʻlchab chiqishimiz mumkin boʻladi.

Shu tariqa tobora maʼlum boʻlib boradiki, sirkul qadami orasi qancha mayda boʻlsa, oʻlchash natijasi shuncha aniq boʻlib boradi.

Fraktallarning cheksiz uzunligi va oʻlchami

Endi esa muhim bir paradoks: sirkul qadami orasi qanchalik mayda boʻlsa, bizga chegara chizigʻi uzunligini oʻlchab chiqish uchun shunga muvofiq koʻproq vaqt talab etiladi. Va “maydalashgan sari uzoqroq” qoidasidagi bu oʻyin cheksiz davom etishi mumkin. Chunki biz chegaraning butun uzunligini sirkulning mayda qadamlariga borgan sari maydaroq qadamlarga boʻlish bilan cheksiz davom ettirishimiz mumkin.

Agar siz chegara hududidagi qishloqlardan biri yaqinida havo sharida osmonga koʻtarilib, c hegaraga nazar solsangiz, siz oʻlchamoqchi boʻlgan butun chegaraning kichik bir boʻlagidan iborat mitti modelini koʻrishingiz mumkin. Bunday oʻlchashlarda, ayniqsa qogʻozga tushirilgan proyeksiyalarda Yevklid geometriyasiga tayanib ish koʻrishga oʻrganib qolganmiz.

Lekin haqiqiy holatda esa bunday oʻlchashlar uchun Yevklid geometriyasi bizga yordam bera olmaydi. Bu oʻrinda biz fraktal geometriyaga murojaat qilishimiz kerak. Yevklid geometriyasida obyektning oʻlchami tushunchasi intuitiv ravishda tushunarli narsa: unda har qanday chiziq bir oʻlchamli. Masalan, elektr simi faqat bir oʻlchamli — uning uzunligi bor xolos. Tekislik esa ikki oʻlchamli —masalan, stol yuzasi shunday. Sfera va shunga oʻxshash uch oʻlchamli jismlarni ham yaxshi bilamiz.

Shuningdek, toʻrt oʻlchamli fazo haqida ham eshitganmiz (nisbiylik nazariyasiga koʻra vaqt toʻrtinchi oʻlcham boʻladi). Fraktallarning oʻziga xos tarafi shundaki, ularning oʻlchami butun son orqali ifodalanmaydi. Masalan, biz oʻlchamoqchi boʻlayotgan chegara chizigʻi oʻlchami 1 yoki 2 emas, 1,25 boʻlishi mumkin. Fraktalning oʻlchamini aniq aytish va matematikadan yiroq boʻlgan oddiy til bilan tushuntirish biroz qiyin.

Lekin bu borada ham ayrim intuitiv tushunarli jihatlar borki, mutaxassisligi matematikadan yiroq boʻlgan odamlarga ham fraktallar haqida umumiy tasavvur bera oladi. Masalan, bir chegara chizigʻi 1,2 fraktal oʻlchamga ega boʻlsa va yana boshqa biri 1,4 fraktal oʻlcham kasb etsa, bundan kelib chiqib, birinchi fraktal bilan belgilangan chegara chizigʻi nisbatan tiniqroq, ikkinchisi esa biroz dagʻalroq ekanini xulosa qilish mumkin boʻladi.

Kantor toʻplami

Eng mashhur fraktallardan biri 1883-yilda toʻplam nazariyasi muallifi Georg Kantor tomonidan tuzilgan. Bu fraktal quyidagicha yasaladi: toʻgʻri chiziq olib, uni uchta teng qismga boʻlamiz va oʻrtadagisini olib tashlaymiz.

Fraktallar geometriyasi: jozibador va beto‘xtov olam

orbita.uz

Keyin xuddi shu jarayonni qolgan ikki qism bilan takrorlaymiz.

fraktallar geometriyasi jozibador va betoxtov olam 2

orbita.uz

Va shu tarzda yana davom etamiz:

fraktallar geometriyasi jozibador va betoxtov olam 3

orbita.uz

Endi tasavvur qiling, ushbu jarayon bir necha ming marta takrorlandi. Oxir-oqibat fraktal strukturaning eng mayda zarra shakllarini ham hosil qilamiz. Kantor fraktalining haqiqiy ahamiyatini matematiklar tushunib yetgunicha ancha vaqt kerak boʻldi. Garchi tashqi koʻrinishidan unchalik ham jozibador fraktal boʻlmasa-da, u eng ahamiyatli fraktallardan biri sanaladi.

Xususan, ushbu fraktal Saturn halqalarining taqsimlanishi singari qiziqarli va muhim fizik hodisalarni oʻrganishga tatbiq qilinadi. Ekonometrikada, narx-navoning keskin oʻzgarishlari yoki raqamli aloqa tizimlarida tarmoqdagi xalaqitlarning yuzaga kelish sabablarini oʻrganishda ham aynan Kantor fraktalidan foydalaniladi. Nil daryosining soʻnggi 2000 yil mobaynidagi sath oʻzgarishlari yoki koinotda galaktika va yulduzlarning joylashish tartiblari ham fraktal strukturalar orqali ifodalanadi.

Menger gubkasi

fraktallar geometriyasi jozibador va betoxtov olam 4

orbita.uz

Rasmda “Menger gubkasi” fraktali. U kubdan undan-da kichikroq kub qirqib olish orqali yasaladi. Keyin esa yanada kichikroq kublar qirqib olinadi va jarayonni cheksiz davom ettirish mumkin. Menger gubkasi qiziq bir xossaga ega: uning sirt yuzasi cheksiz boʻlib, hajmi esa ichkaridan ham, tashqaridan ham nolga teng. Menger gubkasining fraktal oʻlchami 2,72684… ga teng. Bu ajoyib “pishloq” tirqishlar bilan shu darajada toʻlib ketganki, u uch oʻlchamga erisholmaydi. Hozirda ushbu qiziq fraktal model asosida maxsus antennalar ishlab chiqariladi.

Maftunkor Kox qorparchasi

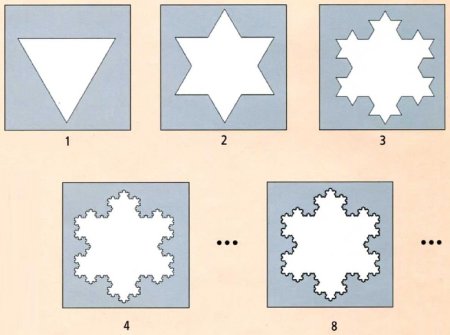
Bu fraktalni 1094-yilda shved matematigi Xelge fon Kox bayon qilib bergan. U teng tomonli uchburchakdan boshlab yasaladi va qorparchaning keyingi shakllanish jarayonining oxiri yoʻq. Rasmda Kox qorparchasini yasashning dastlabki 1,2,3,4 va 8-qadamlari koʻrsatilgan boʻlib, oxirida istalgan marta kattalashtirilganda ham oʻz-oʻzini takrorlovchi strukturaga ega boʻlgan ajoyib fraktal hosil boʻladi.

Agar biz uning perimetrini aniqlamoqchi boʻlsak, unda sezish osonki, shaklning har bir qadamida ushbu qadam hosil qiladigan yangi fraktal shakl perimetri avvalgisidan 4/3 martaga koʻpayadi. Agar boshlangʻich uchburchakning perimetri 3 sm boʻlgan boʻlsa, keyingi qadamlar hosil qiladigan shakl perimetri 4; 5,33… ;7,11…; 9,48…; 12,26… sm va hokazo tarzda kattalashib boradi.

Egri chiziq uzunligi har bir qadam orqali yana va yana kattalashib boradi va demakki, Kox qorparchasining perimetri cheksizdir. Va aksincha, ushbu egri chiziq bilan chegaralangan yuza esa chekli boʻlib, u 2√3/5 ga intiladi. Kox qorparchasining fraktal oʻlchami 1,2619… ga teng.