Entropiya? Bu juda oddiy…

Entropiya. Bu tushuncha ne-ne kallalarni qotirmagan deysiz. To‘g‘rirog‘i, bu tushunchani mohiyatini anglash uchun ne-ne kallalar qotimagan, ne-ne miyalar qiynalib qolmagan deysiz. Chunki, mavzular o‘ta jiddiy izchillik bilan yoritiladigan fizika darsliklarida entropiya tushunchasi biroz murakkab ta’riflanadi. Odatda, entropiya tushunchasining ta’rifini birinchi marta o‘qigan o‘quvchi yoki talaba taxminan quyidagi memda tasvirlangan holatga tushadi.

Keling, shu narsani to‘g‘rilashga urinib ko‘raylik. Ushbu maqolada entropiya tushunchasiga imkon qadar sodda ta’rif berib, uni osonroq tushunadigan qilib izohlashga harakat qilamiz.

Avval boshdan aytish kerakki, entropiya tushunchasi termodinamikadagi bosim, hajm, yoki ichki energiya singari tushunchalaridan sifat jihatdan farq qiladi. Chunki, entropiya bu sistemaning xususiyati emas, balki, ushbu sistemani biz qay tarzda idrok etayotganimizning xususiyatidir. Ya’ni, entropiya aslida bilvosita, subyektiv xossa bo‘ladi. Fikrimcha, entropiyani oson tushunib olishda g‘ov bo‘ladigan eng birinchi holat mana shunda. Ya’ni, termodinamika kurslarida entropiya boshqa obyektiv termodinamik funksiyalar bilan teng tarzda, birgalikda ko‘rib chiqiladi.

Qisqa qilib aytganda, entropiya bu — sistema haqidagi axborotning qanchalik qismi noma’lumligini ifodalovchi xususiyatdir.

Talabalik yillarimizda bir latifa eshitgandim. Moskvada yurgan bir O‘zbek yigitdan bir rus yigiti qayerliksan? Deb so‘raydi. Boyagi O‘zbek yigit «Polvontosh qishlog‘idanman» — deydi. o‘ris yigit ensasi qotib: «Polvontosh qayerd» — deb yana so‘raydi. O‘zbek akamiz ham qizishib, «Polvontosh Marhamatda!» — deydi. o‘ris esa yana battar anglashilmasdan, «Marhamating qayerda?» — deb savolni battar ko‘paytiradi. «Marhamat Andijon viloyatid» — deydi O‘zbek. Shundaginda boyagi o‘ris yigit qarshisidagi odam O‘zbekistondan ekanini tushunadi. Chunki u «Andijon O‘zbekistondami?» — deb so‘raydi. O‘zbek esa «Ha!» deb javob bergach, rus «nega darhol O‘zbekistonlikman demaysan?» — degan ekan… (yaxshiyam, Andijon O‘zbekistonda ekanini o‘risni o‘zi yaxshi bilarkan… )

Bu latifa misolida boyagi rus yigit uchun O‘zbek akaxonimizning qayerdan ekani haqidagi tushunmovchiligi, ya’ni, ma’lumot entropiyasi — Polvontosh qishlog‘ining qayerda ekanidan boshlanib, butun O‘zbekiston haqida aytilganda vaziyat oydinlashishi bilan tugaydi.

Yana bir misol. Agar menga biror odam xorijdan pochta yubormoqchi bo‘lsa va mendan manzilimni so‘rasa, men unga O‘zbekiston deb javob bersam, bu pochta xizmati uchun g‘oyat katta entropiyaga aylanadi. Chunki, O‘zbekistonda millionlab aholi yashaydi va u jo‘natmani aynan kimga berishni aniqlay olmaydi. Endi, men pochta uchun manzilimni yanada aniqlashtirib, unga «O‘zbekiston Respublikasi, Farg‘ona viloyati» desam, vaziyat biroz yengillashadi. Biroq, bunda ham entropiya hali hamon katta. Chunki, garchi, O‘zbekistonning qolgan 11 ta viloyati istisno qilinib, manzil Farg‘onada ekani oydinlashgan bo‘lsa-da, Farg‘onaning o‘zida ham qancha qishloq, mahalla mavjud va pochta uchun baribir bu ma’lumot ham kamlik qiladi. Shu tarzda, men manzilim Marg‘ilon shahri ekanini aytishim, keyin mahallamiz va ko‘chamiz nomini, uy raqamini keltirishim bilan, qaralayotgan masala uchun entropiyani pasaytiraman…

Albatta, yuqoridagi ikkita misol biroz dag‘al o‘xshatish bo‘lib, haqiqiy fizik termodinamik sistemalar bilan taqqoslash biroz g‘alati tuyulsa kerak. Lekin, maqolamizning maqsadi entropiya tushunchasini soddaroq tarzda tushuntirib berish bo‘lgani uchun, bu misollardan foydalanish o‘rinli deb o‘yladik.

Keling yana bir misol ko‘rib chiqamiz. Masalan, menda 10 dona narda toshlari bor. Ularni «gardkam!» deb tashlab, sizga esa, tushgan toshlarning umumiy yig‘indisi 30 ga teng ekanini aytaman va toshlarda aynan qaysi raqamlar tushganini topishingizni so‘rayman. Hozirgi holatda siz buni aniq topa olmaysiz. Chunki sizga ma’lumot kamlik qiladi. Narda toshlaridagi har bir raqamlarni statistik fizika nuqtai nazaridan «mikroholatlar» deyiladi. Umumiy yig‘indini (bizning misolimizda 30 ni) esa «makroholat» deyiladi. 10 ta narda toshi bilan qilingan tajribada 30 sonini olish imkonini beradigan mikroholatlarning jami miqdori 2930455 tani tashkil qiladi. Shunga ko‘ra, mazkur makroholatning entropiyasi taqriban 6,5 ga teng bo‘ladi.

Agar, yana o‘sha 10 ta toshni tashlab, endi tushgan sonlar yig‘indisi 59 ga teng desam, ushbu makroholat uchun faqatgina 10 ta mikroholatlar varianti mavjud bo‘ladi va bunday sistemaning entropiyasi 1 ga teng bo‘ladi. Ko‘rib turganingizdek, turli xil sistemalar, axborotning kam yoki ko‘pligiga qarab, har xil entropiyaga ega bo‘ladi.

Endi, yana o‘sha o‘nta toshni tashlab, ulardan dastlabki beshtasining yig‘indisi 13 ga, qolgan beshtasiniki esa 17 ga teng ekanini aytsam-chi? Bu holatda, hisoblayotgan odam uchun sistemaning entropiyasi yanada pasayadi. Chunki, 5 ta toshdagi raqamlar orqali 13 sonini hosil qilish uchun 420 ta variant mavjud «xolos». Yana qolgan 5 ta toshdagi sonlardan 17 chiqarish uchun esa 780 ta variant mavjud. Shunday qilib, ushbu masala uchun 30 makroholatini olish imkonini beruvchi mikroholatlar miqdori «atiga» 327600 tani tashkil qiladi. Bu esa birinchi misoldagi 2930455 ta variantdan ancha kam. Ya’ni, endi bu safar, sizda sistema haqidagi ma’lumotlar birinchi misoldagidan ko‘ra ancha ko‘proq.

Biz entropiyani makroholatlarning sonini ifodalash uchun ishlatish mumkin bo‘lgan sonlar miqdori orqali o‘lchamoqdamiz. Matematik nuqtai nazardan ushbu miqdor logarifm tarzida aniqlanadi. Shu sababli ham, entropiyani S belgisi bilan belgilab, mikroholatlar sonini esa Ω bilan ifodalasak, entropiyani hisoblash uchun quyidagicha ifoda kelib chiqadi:

S=log Ω

Fizikadan yaxshi xabardor ziyrak mutolaachimiz bu formula Bolsman formulasining aynan o‘zi ekanini darhol fahmladi albatta. Agar makroholat uchun faqat bitta mikroholat varianti mavjud bo‘lsa, bunday sistemaning entropiyasi nolga teng bo‘ladi. Agar, qaralayotgan sistemalar soni ikkita bo‘lsa, ularning umumiy entropiyasi, sistemalarning har birining alohida holda olingan entropiyalarining yig‘indisiga teng bo‘ladi. Chunki, log(AB)=logA+logB

Yuqorida bayon qilinganlardan oydinlashmoqdaki, entropiyani sistemaning o‘z xossasi deb qarash to‘g‘ri bo‘lmaydi. Sistemaning o‘z ichki energiyasi, impulsi, zaryadi va ho kazo asl fizik xossalari bo‘lishi mumkin. Lekin, sistemaning o‘z entropiyasi bo‘lmaydi. o‘nta narda toshlarining entropiyasi ularni tashlagandan keyin tushgan sonlarning yig‘indisiga bog‘liq bo‘ladi. Boshqacha aytganda, entropiya bu — sistemani biz qanday bayon qilayotganimiz (ta’bir joiz bo‘lsa, sistemani biz o‘zimiz qanday idrok qilayotganimiz) ga bog‘liq bo‘ladi. Entropiyaning termodinamikadagi boshqa asosiy tushunchalardan yaqqol ajratib turuvchi jihati ham aynan shunda.

Fizikadan misollar: porshen ostidagi gaz.

Fizika kursida ko‘rib chiqiladigan ko‘hna misollardan biri — porshenli idish ichidagi gazdir. Gazning mikroholati — uning har bir molekulalarining vaziyati va impulsi (tezligi) hisoblanadi. Gazning makroholatni esa, uning bosimi, zichligi, hajmi va kimyoviy tarkibi singari xossalari bilan belgilanadi.

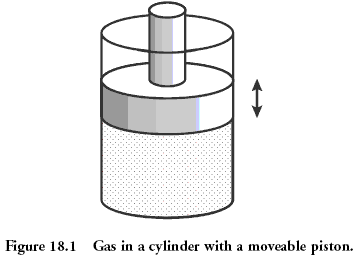
Makroholatni ifodalovchi kattaliklar «holat tenglamasi» orqali o‘zaro bog‘lanishi mumkin. Aynan ushbu bog‘liqlikning mavjudligi, sistemaning mikroholatini bilmasdan turib ham, uni qizdirilsa, yoki, porshen orqali siqilsa, sistemaning ahvoli nima kechishini bilish imkonini beradi. Ideal gaz uchun holat tenglamasi P=ρT ko‘rinishida bo‘ladi. Siz bunga o‘xshash yana bir tenglama — pV = νRT tenglamasini, ya’ni, Mendeleyev-Klayperon tenglamasini yaxshiroq bilarsiz. Lekin, ishonavering, biz yuqorida keltirgan tenglamaning ham ma’nosi aynan shunday. Faqat Mendeleyev-Klayperon tenglamasida qo‘shimcha ikkita konstanta mavjud (va o‘sha konstantalar odamni ko‘proq chalg‘itadi). Berilgan makroholat uchun javobgar mikroholatlar soni qanchalik ko‘p bo‘lsa, ya’ni, sistemadagi zarrachalar soni qanchalik ko‘p bo‘lsa, uning holatini tenglama orqali ifodalash sifati ham shunchalik yaxshi bo‘ladi. Gazlar uchun xos zarrachalar soni Avogadro soniga teng, ya’ni, 10²³ ni tashkil qiladi.

Bosim, harorat va zichlik kabi kattaliklar sistema uchun o‘rtacha qiymatda olinadi. Chunki, bu xossalar haqiqatan ham, sistemadagi bir-birini uzluksiz almashtirib turuvchi mikroholatlarining o‘rtacha qiymatlaridan iborat bo‘ladi. Sistemaning aynan qanday mikroholatda ekanini bilish uchun bizga favqulodda juda-juda ko‘p ma’lumot kerak bo‘ladi. Ya’ni, buning uchun biz sistemani tashkil qiluvchi har bir zarrachaning vaziyatini va tezligini aniq bilishimiz va shuning asosida umumiy sistema uchun qiymatlarni hisoblab chiqishimiz kerak bo‘ladi. Ushbu axborot miqdor entropiya deyiladi.

Makroholatning o‘zgarishi bilan entropiya qanday o‘zgaradi? Buni tushunish oson. Masalan, biz gazni qizdirsak, uni tashkil qiluvchi zarralarning tezligi ortadi. Tezlik oshgani sari, bizning zarrachalar haqidagi bilgan ma’lumotlarimiz kamayib boradi. Yoki, biz porshenni keskin ko‘tarish orqali hajmni orttirsak, gaz molekulalarining joylashuv vaziyati ham darhol o‘zgarib ketadi va ularning vaziyati haqidagi ma’lumotimiz yanada kamayadi. Ya’ni, bilmaganlarimiz ko‘payadi. Demakki, sistemaning entropiyasi biz ichida yana ortadi.