Chasar ko‘pyog‘i

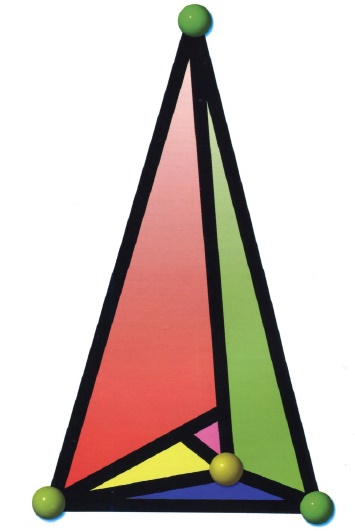Ko‘pyoqlar, yoki, poliedrlar bu — qirralari orqali o‘zaro biriktirilgan ko‘pburchaklardan tashkil topgan uch o‘lchamli jismlar bo‘ladi. Bir yog‘idagi juft uchlarini qaralganda, ular o‘zaro umumiy qirra bilan tutashadigan bo‘lib chiqadigan poliedrlar mavjudmi va ular necha xil? Albatta, bunday poliedrlar mavjud. Lekin ular atiga ikki xil (ikkita) xolos. Yoqlari uchburchaklardan tashkil topgan piramida — tetraedrni odamlar qadimdan yaxshi bilishadi. Tetraedrning istalgan ikkita uchini qarasangiz, ularni umumiy qirra tutashtirib turgan bo‘ladi. Ya’ni, uning diagonallari bo‘lmaydi. e’tibor bering, tetraedrning oltita qirrasi, to‘rtta uchi va to‘rtta yog‘i bo‘ladi.

Shunga o‘xshash, yoqlarini tashkil qiluvchi ko‘pburchaklarning diagonallari bo‘lmaydigan, ya’ni, istalgan ikkita uchini tutashtirib turuvchi umumiy qirraga ega ikkinchi poliedrni 1949-yilda vengr matematigi Akosh Chasar yasashga muvaffaq bo‘lgan. Shuning uchun ushbu ko‘pyoqni Chasar ko‘pyog‘i deyiladi. Faqat, tetraedrdan farqli o‘laroq, Chasar ko‘pyog‘ida tirqish mavjud bo‘ladi. Kombinatorika yordamida aniqlanishicha, diagonallarga ega bo‘lmagan yoqlardan tashkil topuvchi poliedrlar ichida tetraedrdan tashqari boshqa hamma ko‘pyoqlar albatta hech bo‘lmaganda bitta tirqishga ega bo‘lar ekan.

Chasar ko‘pyog‘ini qog‘ozda chizib ifodalash qiyin. Uning modelini yasab qo‘lda ushlab ko‘rgan ma’qul. Yoki, zamonaviy uch o‘lchamli animatsion tasvirlar orqali tomosha qilish ham qulay. Chasar ko‘pyog‘i topologik jihatdan teshikkulcha (tor) ga ekvivalent sanaladi. Ushbu g‘alati va qiziq ko‘pyoqning 7 ta uchlari, 14 ta yog‘i, 21 ta qirrasi mavjud bo‘lib, Silashi ko‘pyog‘ining egizagi deyish mumkin.

Chasar ko‘pyog‘idan keyingi boshqa shu kabi poliedrning aniqlanishi va ayniqsa yasalishi amri mahol. Matematika Devid Darlingning hisoblashicha, shu kabi yana bir poliedr 12 ta yoq, 66 ta qirra va 44 ta uchga ega bo‘lishi kerak. Bunday ko‘pyoqning esa naq 6 ta tirqishi mavjud bo‘ladi! Agar biror o‘ta muhim amaliy foydasi aniqlanmasa, bunday ko‘pyoqni yasashga hech kim urinib ham o‘tirmasa kerak.

Chasar ko‘pyog‘i — diagonallarga ega bo‘lmagan ko‘pburchaklardan yasalgan poliedrlar ichida tetraedrdan tashqari, ikkinchi va hozircha oxirgi ko‘pyoqdir.