Amaliya (Emmi) Nyoter — matematikaning toj-taxtsiz qirolichasi

Zamonamizning saralangan eng yetuk matematiklarining fikricha,
ayollar uchun oliy ma’lumot eshiklari ochilganidan
buyon dunyoga kelganlar orasida Emmi Nyoter
eng yuksak matematik ijodiy iste’dod sohibasi bo‘lgan.

Albert Eynshteyn.

Eynshteyn haq edi. Emmi Nyoter (1882-1935) haqiqatan ham, hayratlanarli darajada o‘ta iste’dodli ajoyib matematik olima bo‘lgan. Eynshteyn Emmi Nyoter bilan Prinston Istiqbolli Tadqiqotlar Institutida birga ishlashni istagandi. Biroq, XX asr fizikasi dahosining bu niyati amalga oshmagan. Ular birgalikda, hamkasb bo‘lib ishlashga muvaffaq bo‘lishmadi. Bunga sabab, Emmi Nyoterning bevaqt o‘limi bo‘lgan edi.

 

Aytish joizki, Emmi Nyoterning matematik iste’dodi borasida Eynshteyn bilan hamfikr bo‘lgan olimlar talaygina edi. Chunonchi, Norbert Viner ham, Emmi Nyoterni o‘sha zamonning yana bir buyuk olimasi, ikkita Nobel mukofoti sohibasi bo‘lgan Mariya Kyuri bilan tenglashtiradi.

Emmi Nyoter haqida Edmund Landau shunday degan edi: «Men uning shubhasiz matematik iste’dodini albatta tan olaman, lekin uning ayol kishi ekaniga ishonishim qiyin». Albatta, Landau ayol jinsiga mansub odamning matematikadan bu darajada iste’dodli bo‘la olishiga ishonolmaganiga urg‘u bermoqchi bo‘lgan. Biroq, uning hazil aralash aytgan ushbu gapida biroz kinoya ham mavjud. Haqiqatan ham, Emmi Nyoter tashqi ko‘rinishi jihatdan biroz ayollarga xos bo‘lmagan xususiyatlar egasi bo‘lgan. U juda gavdali, yelkalari keng, ovozi yo‘g‘on, qisqasini aytganda, erkakshoda ayol bo‘lgan edi. Emma shuningdek, odatiy ayollardan farqli ravishda, o‘z tashqi ko‘rinishiga unchalik ham jiddiy e’tibor bermaydigan, odmi, to‘pori ayol bo‘lgan. Ayniqsa, u o‘zi tekshirayotgan biror matematik masalaga berilib ketgan paytlarda, yoki, ilmiy munozaralar chog‘ida, ayollarga xos bo‘lgan har qanday nazokat va uyatchanlikni bir chetga surib qo‘yib, vaziyatga jon-jahdi bilan kirishib ketardi. Emmi Nyoterni yaqindan tanigan odamlar, uni odatda sochlari tartiblanmagan, kiyimlarni ham pala-partish kiyadigan, ovqatni ham yaxshi chaynamasdan, chapillatib, yutoqib yeydigan ayol sifatida eslab qolishgan. Albatta, ayniqsa u yashagan o‘ta tartibli nemis jamiyatida, bu kabi holatlar «madaniyatsizlik» deb qaralardi va shuning uchun, Emmini ko‘pchilik yoqtirmasdi. Ustiga-ustak, Emmi Nyoter deyarli butun umri davomida linzalari juda qalin va katta-katta bo‘lgan ko‘zoynak taqib yurgan. Olima yaqinni ko‘ra olmaydigan ko‘z xastaligidan aziyat chekardi. Ko‘zoynaklari uning yuzini deyarli yarmini to‘sib turardi va shunga ko‘ra ayrim g‘alamislar Emmiga «boyqush« deb laqab qo‘yishgan. Biroq, Emmining o‘zi, xuddi o‘z tashqi ko‘rinishiga befarq bo‘lganidek, o‘zi haqidagi bu kabi uzun-quloq gaplarga ham mutlaqo beparvo ayol bo‘lgan. Uning uchun kiyimlar va buyumlarni tanlashdagi yakkayu-yagona mezon — faqat qulaylik bo‘lib, olimani moda va boshqa urfga kirgan narsalarga qiziqqanligini birov ko‘rmagan. Shu xislatiga ko‘ra, Emmi odatda boshiga erkaklar shlyapasini kiyib yurardi. Shuningdek, olimaning qo‘lida ichi doimo turli qog‘ozlar va matematika kitoblari bilan liq to‘la yuradigan katta qora chamadoni bo‘lardi. Tasavvur qiling: gavdali, ovozi yo‘g‘on, sochi betartib, bir-biriga mos bo‘lmagan kiyimlarni kiyib, boshiga shlyapa qo‘ndirib olgan, qo‘lida katta qora chamadon ko‘targan nemis ayoli! Emmi Nyoter aynan shunday ayol bo‘lgan!

Emmi Nyoterning eng iste’dodli shogirdlaridan bo‘lgan German Veyl, o‘zining to‘pori ustozi haqida shunday degan edi: «U nazokat va latofatdan keyin tug‘ilgan«.

Amaliya Nyoterning yoshligidagi portreti

Serviqor oqqushga aylanish

Ta’bir joiz bo‘lsa, Emmi Nyoter — ayollarning oyoq-qo‘llari kishanlangan jamiyatda tug‘ilgan deb aytish mumkin. o‘sha vaqtlarda Germaniyani dabdabali ziyofatlar va marosimlar ishqibozi bo‘lgan, qudratli kayzer Vilgelm II boshqarardi. Kayzer odatda biror shaharga poyezdda tashrif buyurar, u vagondan tushib kelayotgan paytda esa, mahalliy shahar hokimi tantanali nutq so‘zlab, yuksak martabali mehmonni qutlab kutib olishi kerak bo‘lgan. Mamlakatning ichki va tashqi ishlari bilan bog‘liq barcha og‘ir-yengil ishlarni esa, «Temir Kansler» nomini olgan Otto fon Bismark yuritardi. Bismark tom ma’noda, davlat va jamiyatning yetakchisi bo‘lib, u Germaniyaning konservativ strukturasini saqlab qolish tarafdori bo‘lgan. Bismarkning tushunchasiga ko‘ra, jamiyatda ommaning yoppasiga savodli-ma’lumotli bo‘lishi — nomaqbul tuzum — sotsializmning belgisi hisoblanardi. Shu sababli, Bismark boshchiligidagi hukumat, ayollarning oliy ma’lumot olishini unchalik ham xushlamaydigan konservator amaldorlardan iborat bo‘lgan.

XIX va XX-asrlar chegarasida yashagan nemis xotin-qizlari uchun ideal ayol timsoli sifatida, kayzerning xotini — imperatritsa Avgusta Viktoriya qiyofasi ko‘rsatilardi. Imperatritsaning hayot falsafasi esa, «to‘rt K» shaklida bo‘lib, quyidagicha yangragan: K — kayzer; K — Kinder (ya’ni, bolalar); K — Kirche (cherkov); K — K»che (oshxona). Tabiiyki, oddiy nemis ayollari uchun ham, imperatritsaning ushbu maslagi o‘rnak qilib ko‘rsatilgan va uni xalqqa singdirishga uriniligan. Bunday muhitda esa, jamiyatda deyarli hamma ayollarning o‘rni, xuddi oldindan qat’iy belgilab qo‘yilgan ssenariy singari, faqat muayyan maishiy yumushlarni bajarish bilan cheklanib qolavergan. o‘sha zamonda yashagan bir nemis jamiyatshunosining ta’biri bilan aytganda, nemis ayollarining ijtimoiy darajasi erkaklarnikidan pastda va uy hayvonlarinikidan tepada bo‘lgan…

Albatta, o‘sha Germaniyada ayollarning ta’lim olishi butunlay ta’qiqlangan edi deb bo‘lmaydi. Harholda, oliy ma’lumot olishni istagan ayollar uchun muayyan sharoitlar bo‘lgan. Lekin, umuman olib qaraganda, ayollarning ta’lim olishga bo‘lgan imkoniyati yo‘q hisobi edi. Agar, mabodo ta’lim olish ishtiyoqidagi biror qiz, bu yo‘ldagi barcha o‘g‘ir va yengil to‘siqlarni yengib o‘tib, oxir-oqibatda oliy ma’lumotga erishsa hamki, uning keyinchalik biror tayinli ish topishi, ayniqsa, qandaydir lavozimlarda ishlashi imkonsiz bo‘lgan. xullasini aytganda, o‘qigan va o‘qimagan qiz uchun yakun deyarli bir xil bo‘lib qolavergan. Ta’lim muassasalarida esa, ayrim o‘ta keskin tushunchali o‘qituvchilar, auditoriyada bir dona bo‘lsa ham, ayol kishi o‘tirgan bo‘lsa, darsni boshlamay turaverishgan. Ular, ilm-fan faqat erkaklarga tegishli mashg‘ulot deb qat’iy turib olishardi va ma’ruza tinglamoqchi bo‘lgan qizlarni xonadan chiqib ketishini kutib turishardi.

Emmi Nyoter 1882 yilning 23-martida, shunday biryoqlama g‘aliz tushunchalarga ko‘milib yotgan Germaniyaning Erlangen shahrida dunyoga kelgan. Uning ota-onasi jamiyatning o‘rta qatlamiga mansub oddiy o‘qituvchilar bo‘lishgan. Erlangen — Emmi Nyoterdan tashqari, dunyoga yana Xristian fon Shtaudt (1798-1867) hamda, Feliks Klyayn (1849-1925) singari yetuk matematiklarni ham yetkazib bergan mo‘jaz shaharcha bo‘lib, shuningdek bu shahar nomini matematikada Feliks Klyayn shakllantirgan «Erlangen dasturi» nomli tushuncha ham mashhur qilib turibdi. Ushbu dasturda Feliks Klyayn geometriyani guruhlar nazariyasi nuqtai nazaridan qayta tasniflaydi.

Emmi Nyoterning otasi Maks Nyoter Erlangen universitetida matematikadan dars bergan. Maks Nyoter ham yoshligidanoq kuchli matematik iste’dodi bilan ajralib turgan ekan. Otasining ajoyib matematik salohiyatini Emmidan avval uning akasi Frits Nyoter ham o‘zlashtirgan bo‘lib, u ham o‘z hayotini ushbu ajoyib fanga bag‘ishlagan. Frits Nyoter amaliy matematika bilan shug‘ullangan.

Emmi Nyoterning yoshligini xuddi Gans Xristian Andersenning mashhur «Irkit o‘rdakcha« nomli ertagiga qiyoslash mumkin. Ushbu qizaloqni, kelajakda balki butun matematika fani tarixidagi eng yetuk ayol matematik bo‘lib yetishishini hech kim, hatto o‘z ota-onasi ham tasavvur qilmagan bo‘lsa kerak. Biroz beso‘naqayligini aytmaganda, bolaligida Emmini boshqa nemis qizlaridan yaqqol ajratib turadigan biror jihati bo‘lmagan. U ham, oddiy o‘smir qizlar kabi, raqs tushishni juda yaxshi ko‘rgan va raqsbop ashula yangraydigan har qanday tantanalarga borishni kanda qilmagan. Lekin, u boshqa matematiklardan farqli ravishda, bolaligida ham, keyinchalik ulg‘ayganda ham, hech qachon musiqaga ixlos qo‘ymagan. Biz odatda ko‘plab yetuk matematiklarning musiqani juda yaxshi ko‘rganliklarini, ba’zilari esa, ayrim musiqa asboblarida professional kuy ijro eta olganliklarini yaxshi bilamiz. Biroq, Emma haqida bunday deyishning iloji yo‘q. Emma va uning oilasi kelib chiqishiga ko‘ra yahudiylar bo‘lishgan. U tug‘ilib katta bo‘lgan paytlarda Germaniyada hali odamlarning millati va diniga qarab ajratish, ya’ni, fanatik millatchilik deyarli yo‘q darajada bo‘lgan. Biroq, baribir bu narsa keyinchalik olimaning taqdiriga o‘z ta’sirini o‘tkazmay qolmadi (bu haqida quyiroqda batafsil).

Muayyan epizodlarni inobatga olmaganda, Emmi Nyoterning maktab ta’limidagi o‘zlashtirish darajasi ham boshqa tengdoshlarinikidan keskin farq qiluvchi qandaydir alohida e’tiborga molik darajada bo‘lmagan. Manbalarda uning o‘smirlik yillarida uy- xo‘jalik ishlarini juda qoyil qilib do‘ndirib qo‘ygani va maktabda xorijiy tillar (fransuz va ingliz tillari) bo‘yicha a’loga o‘qigani ta’kidlanadi xolos. Emmining chet tillarini o‘zlashtirishdagi ko‘rsatkichlarini inobatga olgan holda, o‘qituvchilari unga kelajakda chet tili o‘qituvchisi kasbini tanlashni maslahat berishgan ekan. Lekin, hammani hayron qoldirib, Emmi chet tillari yo‘nalishini emas, balki, matematikani tanladi.

Poyonsiz poyga

o‘z umrini matematikaga bag‘ishlash uchun Emmida hamma narsa bor edi: matematika u uchun alifbodek gap bo‘lgan; oilasi Emmining o‘qishi uchun, garchi ancha kamtarona bo‘lsa-da, harholda kerakli mablag‘ bilan ta’minlay oladigan holatdagi, o‘ziga to‘q xonadon bo‘lgan. Qolaversa, Emmi otasi orqali mahalliy universitetning deyarli barcha o‘qituvchilari bilan shaxsan tanish bo‘lib, bu holat uning universitetda biroz erkin ta’lim olishiga sharoit hozirlagan.

Matematikadan oliy ma’lumotga ega bo‘lish uchun Emmi universitetga tinglovchi maqomida qatnashiga to‘g‘ri kelgan. Uning oliy o‘quv yurtining to‘laqonli talabasi bo‘lishga huquqi bo‘lmagan. Shunga qaramay, Emmi Nyoter universitetdagi barcha imtihonlarni muvaffaqiyatli topshirib, doktorlik darajasi olish imkonini qo‘lga kiritgan. o‘z doktorlik ishi uchun Emmi ternar kvadrat shakllarning algebraik invariantlari mavzusini tanlagan. Erlangenda ushbu yo‘nalishda ta’lim beradigan mutaxassis — Paul Gordan (1837-1912) ismli matematik bo‘lib, u shuningdek Emmining otasi Maks Nyoter bilan yaqin do‘st bo‘lgan. Zamondoshlari Paul Gordanni «invariantlar qiroli» deyishardi. Gordan ushlagan joyidan uzadigan, o‘ta injiq, lekin nihoyatda puxta ish yuritadigan matematik bo‘lgan. Boshqa matematiklarning toqati yetmaydigan, yoki, foydasiz deb hisoblab tashlab qo‘yadigan uzundan-uzoq hisoblashlarni ham, Gordan sabr bilan, qancha kerak bo‘lsa, shuncha vaqt sarflab sinchiklab bajarib chiqishi, keyin esa, natijani ham erinmay bir boshdan, boshqatdan tekshirib chiqishi odatiy hol bo‘lgan. Algebraik invariant va shaklning nima ekanligini tushuntirish unchalik ham qiyin emas. Lekin, zamonaviy matematika uchun ushbu tushunchalar dolzarbligini yo‘qotgan va shu sababli, ular haqida mufassal to‘xtalib o‘tirmaymiz.

Emmi Nyoter o‘zining «Ternar bikvadratik shakllarning shakliy tizimlarini aniqlash haqida» deb nomlangan doktorlik dissertatsiyasida, jami 331 xil o‘zi topgan invariantlarni keltirib o‘tgan. U doktorlik dissertatsiyasini katta muvaffaqiyat bilan himoya qilgan. Mazkur ilmiy ish unga matematika bilan professional shug‘ullanish imkonini bergan bo‘lsa-da (aslida bunday imkon doim bo‘lgan), lekin, aytaylik, biror oliy o‘quv yurtida to‘laqonli ishlab, dars berish huquqini taqdim qilmagan. Fan doktori bo‘lgan Emmi Nyoterga Erlangen universitetining o‘zida matematikadan dars taklif qilishgan. Biroq, aytganimizdek, bu ish to‘laqonli bo‘lmay, balki, faqat bir tomonlama majburiyat bajarish bilan cheklanuvchi ish edi. Ya’ni, Emmiga ming mashaqqat bilan o‘tadigan ko‘p soatlik darslari uchun sariq chaqa ham haq to‘lanmagan. U o‘ziga yuklatilgan va tekinga o‘tiladigan dars soatlaridan tashqari, vaqti-vaqti bilan otasining darslarini ham o‘tib turishiga to‘g‘ri kelardi. Chunki, bu paytga kelib ota Nyoterning salomatligi ancha yomonlashib qolgandi va u ba’zan universitetga borib kelishga ham yaramay qolardi. Shunday g‘alati va murakkab mehnat sharoitida Emmi Nyoter naq 8 yil mehnat qilib, talabalarga matematikadan dars bergan. Olimaning o‘zi o‘sha paytdagi faoliyatini hazil aralash «matematik gimnastika» deb atardi. Garchi Emmi Nyoter Germaniyada Sofya Kovalevskayadan keyin matematikadan fan doktori darajasiga erishgan ikkinchi ayol bo‘lgan bo‘lsa-da, biroq, ushbu daraja amalda unga deyarli hech narsa bermagan. Emmi keyinchalik o‘z ilmiy faoliyatini tahlil qilayotgan paytlarda, o‘sha — yillarni eslab «bema’nilik» deb qo‘yardi.

Vaqt o‘tishi bilan Nyoterning ustozi Gordan nafaqaga chiqib ketadi. Uning o‘rniga esa universitet ma’muriyati Ernst Fisher ismli yosh matematik mutaxassisni ishga tayinlaydi. Fisher jamiyatda ayollarning ham tenghuquqli ta’lim olishi tarafdori bo‘lib, u o‘z mutaxassisligini puxta egallagan, ilg‘or fikrli kishi edi. Emmi Nyoter va Ernst Fisher ham professional-kasbiy yo‘nalishda, ham ishdan tashqari hayotda nihoyatda yaqin do‘st va hamkasb bo‘lib qolishgan.

Ernst Fisher o‘z davrining eng yetuk matematiklari — David Gilbert va Feliks Klyayn bilan shaxsan tanish bo‘lib, u mazkur matematika daholariga o‘z hamkasabasi Emmining beqiyos matematik iste’dodi haqida so‘zlab bergan. Biroz vaqt o‘tib, Fisher Emmi Nyoter va David Gilbertlarni o‘zaro tanishtirib qo‘yadi. Gilbert va Klyayn Emmining qay darajada yuksak matematik iste’dod sohibasi ekanligini darhol payqashgan va ilmiy tadqiqotlarni birgalikda olib borish istagini bildirishgan. Ushbu ikki matematik olimlar, «jahonning eng matematik universiteti» deb sharaflanuvchi Gyottingen universitetida mehnat qilishar edi. Ularning har ikkalasi ham, ayollarning erkaklar bilan tenghuquqli ta’lim olishi va ilmiy tadqiqotlarda to‘laqonli ishtirok etishi tarafdori bo‘lishgan.

Yevropani o‘z domiga tortgan birinchi jahon urushining eng avj pallasida, ya’ni, 1915-yilda Gilbert va Klyayn birgalikda zo‘r berib harakat qilib, Emmi Nyoterni Erlangendan Gyottingenga ko‘chib o‘tishga ko‘ndirishga muvaffaq bo‘lishdi. Ayni shu yillarda butun dunyo ilm-fanida Eynshteynning inqilobiy g‘oyalari muhokama qilinmoqda edi. Gilbert esa, Emmining algebraik invariantlar bo‘yicha kuchli mutaxassis ekanligini inobatga olib, uning invariantlar bo‘yicha ishlanmalarini Eynshteynning nazariyalarining isboti uchun kuchli matematik apparat sifatida tadbiq etishni ko‘zlagan (bu haqida keyinroq yana to‘xtalamiz).

Albatta, bularning hammasi Emmi uchun porloq kelajak va’da qilayotgandek edi. Bir qarashda juda silliq boshlangan Gyottingen hayoti juda tezkorlik bilan sarobga aylandi. Qanchalik nufuzli olim bo‘lmasin, na Gilbert va Klyayn Emmi Nyoter uchun Gyottingen universitetdan muqim ish o‘rni topib bera olishmadi. Aniqrog‘i, ular taklif qilgan benazir matematik ayolni universitet ilmiy kengashi o‘z safiga qo‘shishni istamadi. Nyoterga Gyottingen universitetida to‘laqonli ishlash imkoni berilmasligi uchun yagona bahona — uning shunchaki ayol kishi ekanligi bo‘lgan. Chunonchi, universitet rahbarlaridan biri Gilbertga bu borada raddiya berar ekan: «Urushda qahramonlarcha jang qilayotgan askarlarimiz vatanga qaytishganida, auditoriyalarda o‘tirgan va dars berayotgan ayol kishini ko‘rishsa nima degan odam bo‘lamiz? Ularga ayol kishi dars bersa qanday holga tushishadi?». Bu kabi bo‘lmag‘ur ta’nalarni eshitishdan toqati toq bo‘lgan Gilbert ham, o‘ziga xos bo‘lmagan ravishda keskin fikr bildirishga majbur bo‘lgan: «Men hecham tushunolmayman, nima uchun nomzodning jinsi uni biror ishga tayinlanishiga xalaqit berishi kerak? Axir biz erkaklar hammomida emas, universitetda ishlaymiz-ku?!«

Gilbert Emmi Nyoterga Gyottingen universitetida privat-dotsent bo‘lib ishlashni taklif qilgan edi. Lekin, yuqorida ham aytganimizdek, Gilbert darajasidagi nufuzli olimning tavsiyasi va aralashuvi ham universitet ma’muriyatidagi eskicha qarashlar asosida biryoqlama fikrlaydigan tepsa tebranmas korchalonlarning tushunchasini o‘zgartira olmadi. Ular Emmini baribir ishga qabul qilishmagan. Aksincha, universitet ilmiy kengashi, Gilbertning zo‘r berib urinishlariga qarshi ravishda, Emmi nomzodini zo‘r berib inkor etardi. Ziddiyatlarga faqatgina Germaniyada davlat tuzumining o‘zgarishigina barham bergan: mamlakatda Veymar Respublikasi e’lon qilinishi bilan, ayollarning jamiyatdagi o‘rni va ta’lim olish huquqi borasida ancha ijobiy islohotlar o‘tkazilgan. Natijada, Emmi uchun Gyottingenda ishlashga to‘siq bo‘lib turgan g‘ovlar olib tashlandi. Emmi Gyottingenda matematika professori sifatida ishlay boshlagan. Biroq, bu safar ham unga ish uchun maosh tayinlashmagan. Shu tariqa, olima faqatgina o‘z ishtiyoqi va matematikaga bo‘lgan muhabbatiga tayanib, universitetda tekinga dars berib kelgan. Uning bu tariqa faoliyati to 1922-yilgacha davom etdi. Faqat shu yilga kelibgina universitet ma’muriyati olimaga ish haqi to‘lay boshlagan. Emmi Gyottingenda tekinga dars berishdan tashqari, «Matematika solnomalari» («Mathematische Annalen») jurnaliga ham muharrirlik qilgan bo‘lib, olimaga ushbu ma’suliyatli ish uchun ham haq to‘lanmagan.

1918-yilda Emmi Nyoter o‘z nomi bilan ataluvchi sensatsion teoremani e’lon qildi. Garchi Emmi hayoti matematik faoliyati davomida boshqa ko‘plab va muhim teoremalarni isbotlagan bo‘lsa-da, lekin mutaxassislar uning aynan o‘sha, 1918-yilda isbotlagan teoremasini «Nyoter« teoremasi deb atay boshlashgan. Aslida Emmi mazkur teoremaning isbotini uch yil avvalroq, ya’ni, 1915-yildayoq topgan bo‘lib, qandaydir sabablarga ko‘ra uni e’lon qilishni orqaga surib kelgan edi. Nyoter teoremasi mavhum algebra sohasiga tegishli bo‘lib, u fizika va matematika fanlari uyg‘unlashgan nuqtaga, aniqroq aytganda esa, mexanika sohasiga taaluqlidir. Nyoter teoremasini tushunish uchun o‘quvchida oliy matematika va fizika fanlaridan mustahkam bilimlar egasi bo‘lish talab etiladi. Shu sababli, kitobxonni ushbu teorema bilan batafsil tanishtirib o‘tirishni ma’qul topmadik. Qiziquvchilar bu boradagi kerakli ma’lumotlarni kutubxonalardan va internet sahifalaridan o‘zlari topa oladilar degan umiddamiz.

Agar oddiy kitobxonni cho‘chituvchi matematik formulalar va belgilashlarsiz, oddiy til bilan bayon qiladigan bo‘lsak, Nyoter teoremasining qisqacha ta’rifi quyidagicha yangraydi: «Agar fizik sistema uzluksiz simmetriyaga ega bo‘lsa, unda o‘z qiymatini vaqt bo‘yicha saqlab turadigan mos kattaliklar albatta mavjud bo‘ladi«.

Uzluksiz simmetriya tushunchasini oliy fizika kursida Li guruhlari orqali tushuntiriladi. Oliy fizikada, simmetriya deyilganda, sistemaning fizik kattaliklari sistemadagi istalgan o‘zgarishlarga nisbatan invariant bo‘ladigan holat tushuniladi. Sistemadagi ushbu o‘zgarishlar uzluksiz matematik o‘zgartirishlar vositasida qaralganida butun sistemaning koordinatalarini keltirib chiqarishi kerak bo‘ladi; qaralayotgan fizik kattaliklar esa, sistemadagi o‘zgarishlardan avval ham, keyin ham o‘z qiymatini saqlashi, ya’ni, o‘zgarmasdan qolishi lozim.

«Simmetriya« atamasi qayerdan kelib chiqqan? Ushbu atama aslida sof fizik tushuncha bo‘lib, matematikadagi simmetriya bilan ma’no jihatdan o‘xshash bo‘lgani uchun keng qo‘llaniladi.

Nyoter teoremasiga ko‘ra, agar fizik sistema o‘xshash uzluksiz simmetriyaga nisbatan invariant bo‘lsa, demak, bunday fizik sistemada albatta u yoki bu fizik kattalikning saqlanish qonuniyati mavjud bo‘ladi. Tasavvur qilish uchun, fazoda tegishli simmetriyalar guruhini tashkil qiluvchi burilishlarni ko‘z oldingizga keltiring. Agar, shunday burilishlardan birini koordinatalar sistemasiga tadbiq qilsak, unda boshqa bir yangi koordinatalar sistemasi kelib chiqadi. Koordinatalarning o‘zgarishlari esa tenglamalar vositasida ifodalanadi. Bunday holatda, Nyoter teoremasiga ko‘ra tegishli algebraik hisob-kitoblarni bajarsak, tasavvurimizdagi burilishlardan iborat simmetrik fizik sistemada saqlanish qonuniga ega bo‘ladigan fizik kattalik impuls bo‘lishni bilib olamiz. Ushbu mavzuda chuqurlashmasdan, quyida simmetriyaning ayrim turlari haqida qisqa ma’lumot keltirish bilan cheklanamiz. Jadvalda simmetriya, simmetriya guruhlari va tegishli simmetriya guruhida albatta o‘zgarishsiz saqlanadigan (saqlanish qonuniga ega bo‘ladigan) fizik kattaliklar keltirilgan:

Simmetriya, yoki, simmetriya guruhi	Saqlanuvchi fizik kattalik
Vaqt bo‘yicha ko‘chish	Energiya
Fazo bo‘yicha ko‘chish	Impuls
Fazo bo‘yicha burilish	Impuls momenti
CTP	Juftliklar hosilasi
U(1)	Elektr zaryadi
U(2)	Kuchsiz elektr o‘zaro ta’sirdagi kuch
SU(2)	Izotopli spin
SU(3)	Kvark rangi
U(1)×SU(2)×SU(3)	Kvant fizikasining standart modeli

Nyoter teoremasi yuqorida ham aytganimizdek, butun dunyodagi yetakchi ilmiy doiralarda katta sensatsiyaga sabab bo‘lgan. Jahonning eng yetakchi va nufuzli olimlari Nyoter teoremasi haqida mazmuni maqtov va hayratdan iborat ko‘plab fikrlarni bildirishgan. Chunonchi, Nyoter teoremasi bilan tanishar ekan, Albert Eynshteyn ham o‘z hayratini yashirolmay qolgan bu haqida Gilbertga shunday yozgan edi:

«Kecha men Nyoter xonim muallifligidagi, invariantlarni yasashga bag‘ishlangan juda qiziq maqola bilan tanishdim. Meni hayratga solgan narsa shuki, bunday murakkab tushunchalarni shu darajada umumlashtirib qarashning iloji bor ekan. Gyottingenning eski Gvardiyasini ta’lim olish uchun aynan Nyoter xonim huzuriga yuborish kerak deb o‘ylayman. U o‘z hunarini mukammali bilar ekan«.

Albatta, Eynshteynning maqtov va hayratlari bejiz emasdi. Chunki, aynan Nyoter teoremasidan foydalanib, Eynshteyn umumiy nisbiylik nazariyasi bo‘yicha hal qilinishi lozim bo‘lgan ko‘plab masalalarga yechim topgan. Jahon matematikasining Emmi Nyoter bilan bir vaqtda va undan keyin yashab o‘tgan ko‘plab yirik namoyandalari, shuningdek, hozirgi zamonamizning eng yuksak salohiyatli matematiklari ham, Nyoter teoremasini xuddi Pifagor teoremasi singari, matematikadagi fundamental teoremalar turkumiga kiradi deb e’tirof etishadi.

Keling, Karl Popper (1902-1994) tomonidan bayon qilingan, oddiy va tushunarli tajribalar olamiga birozga nazar tashlaymiz. Unda biz, muayyan fizik hodisaning mohiyatini ifodalovchi qandaydir yangi bir nazariyani barpo qildik deb tasavvur qilamiz. Nyoter teoremasiga ko‘ra, agar biz barpo qilgan o‘sha nazariyada simmetriyaning biror bir ko‘rinishi mavjud bo‘lsa, unda mazkur sistemada albatta doimiy saqlanuvchi qandaydir fizik kattalik mavjud bo‘ladi. o‘sha kattalikni o‘lchash va uning saqlanish qonuniyatini aniqlash orqali, biz o‘zimiz barpo qilgan nazariyaning haq yoki nohaqligini tekshirib olishimiz mumkin bo‘ladi.

Nyoter teoremasi

Mexanika sohasida fizik sistemaning ta’rifi anchayin murakkab atama va tushunchalar orqali keltiriladi. Masalan, unda harakat deganda, ajralib chiqqan energiya bilan, ushbu energiyaning yutilishi uchun sarflangan vaqtning ko‘paytmasi tushuniladi. Fizik sistemaning holatini matematik tilda ifodalanishi uning lagranjiani (L) orqali bayon qilinadi. Lagranjian — ko‘rinishidagi funksional, ya’ni, funksiyaning funksiyasi tarzida bo‘ladi. Bunda q — vaziyat; q’, tezlik (belgi tepasidagi nuqta Nyuton notatsiyasiga ko‘ra, q ga ko‘paytmani bildiradi); t esa — vaqt. e’tibor qarating, q — umumiy koordinatalar sistemasidagi vaziyat bo‘lib, u albatta dekart sistemasi bo‘lishi shart emas.

Misol uchun, biror A harakat matematika tilida sistema tanlagan yo‘l bo‘yicha olingan integral orqali quyidagicha ifodalanadi:

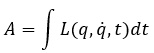
XIX asr fizikasida juda katta ahamiyat kasb etgan «eng kichik harakat» tamoyiliga ko‘ra, fizik sistema eng kam kuch sarflanadigan yo‘nalish bo‘yicha harakatlanadi. Shunga ko‘ra, agar matematik analiz tili bilan aytadigan bo‘lsak, qaralayotgan A harakatning qiymati ekstremal qiymat, ya’ni, yoki maksimum, yoki, minimumni tashkil etishi kerak. Shu sababli, uning dastlabki hosilasi nolga teng bo‘lishi kerak.

Bitta yaxshi ko‘rgazmali tushuntirish, mingta quruq gapdan yaxshiroq deyishadi. Keling, Nyoter teoremasini bir amaliy misol vositasida ko‘rib chiqamiz:

Tasavvur qilamiz, zarrachalar sistemasi qandaydir bir simmetriyaga ega bo‘lib, uning L lagranjiani, sistemadagi qandaydir s fizik kattalikning o‘zgarishlariga nisbatan invariant. Ya’ni, . Unda, sistemaning tarzida saqlanadigan C xossasi ham mavjud bo‘ladi.

 

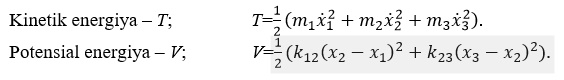
Bu o‘rinda umumiy koordinatalar q, dekart koordinatalari bo‘lmish x_i bilan mos tushmoqda. Matematik analiz usullarini, xususan, Eyler-Lagranj tenglamasini qo‘llash orqali ga ega bo‘lamiz.

Endi simmetriyani qaraymiz. Teorema ta’rifida u s bilan belgilangan. Yuqoridagi ifodalarimizga ko‘ra, elastiklik qonuni bajarilayotganligi sababli, biz s=t ekanini taxmin qilishimiz mumkin bo‘ladi; ya’ni, vaqt va boshlang‘ich ta’rifda keltirilgan lagranjianning simmetriyasi quyidagicha namoyon bo‘ladi:

Ba’zi algebraik shakl almashtirishlarni keltiramiz:

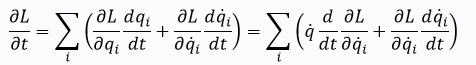
Hadlarni qisqartirish orqali

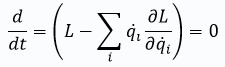
ga ega bo‘lamiz.

Ushbu ifoda orqali biz saqlanish qonuniyatiga ega bo‘lgan fizik kattalikni, ya’ni, C ni keltirib chiqardik. U ifodaning qavslar ichidagi qismida yashiringan. bo‘lgani uchun,

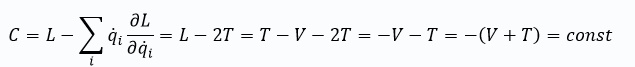
ekanligi kelib chiqadi.

Ifodadagi kinetik va potensial energiyalarning yig‘indisi (manfiy ishorali), ya’ni, sistemaning umumiy energiyasi -doimiydir. Demak biz, energiyaning saqlanish qonunini keltirib chiqardik!

 

Algebra va faqat algebra. Qandayin algebra!

Biz Emmi Nyoter haqidagi hikoyamizni, uning qanday qilib jahonning eng nufuzli matematika universitetida — Gyottingenda, matematika fanining eng yorqin yulduzlari bo‘lmish David Gilbert va Feliks Klyaynlar bilan ish boshlagan joyida to‘xtatgan edik. Gilbert Emmiga universitetda dars o‘tish imkoni berilishi turli bahonalar bilan paysalga solinib kelayotgan patlarda, shunday kuchli olimaning bilimini boshqa talabalarga ham ulashish uchun ajoyib, yaxshi ma’nodagi ayyorona yo‘l o‘ylab topgan. U dars jadvaliga va darsdan tashqari mashg‘ulotlar ro‘yxatiga o‘z nomi bilan qator ma’ruza va kurslar kiritib qo‘yadi. Lekin, ushbu ma’ruza va kurslarni Gilbertning o‘zi emas, balki, Emmi Nyoter o‘tardi. g‘alamislarga esa, bu holatga qanday barham berish haqida bosh qotirib yurishdan boshqa ish qolmaganday edi go‘yo.

Emmi Nyoter juda mehnatsevar va ishchan ayol bo‘lgan. Ko‘pchilik hamkasblari uni tormozi ishdan chiqqan avtomobilga o‘xshatishardi. Emmi har kuni soatlab tik oyoqda dars o‘tishi, darsdan keyin ham, istalgan mutaxassis bilan, (ko‘pincha Gilbert bilan) dolzarb masalalar borasida uzundan-uzoq munozaralar olib borishi odatiy hol bo‘lgan. U charchoq nimaligini bilmaydigan, o‘z ishini — matematikani jon-dildan sevadigan olima bo‘lgan.

1920-yilda Emmi o‘zining ilmiy tadqiqot yo‘nalishini biroz o‘zgartirishga qaror qiladi. U asta-sekinlik bilan bor e’tiborini sof algebra masalalariga qarata boshladi: avvaliga uning diqqat markazida halqalar va halqalardagi ideallar masalasi bo‘lgan; keyinroq u yanada murakkab strukturalarni tadqiq qilishga o‘tib ketgan. Emmi o‘zi ish olib borgan halqalar mavzusini shu darajada puxta egallab olganki, uni ba’zi matematiklar hazil aralash «uzuklar hukmdori» bo‘lgan ham deyishadi. Uning bu davrdagi ilmiy ishlari samarasi o‘laroq, Lasker-Nyoter teoremasi (1921), hamda me’yorlashtirish haqidagi lemma (1926) singari muhim tushunchalar matematika faniga kirib kelgan. 1927-yilda esa u izomorfizm haqidagi teoremani shakllantirgan.

Keyin esa, Emmi matematikaning yanada murakkabroq yo‘nalishlariga bosh suqib ko‘radi. U murakkablik pog‘onalaridan yuqorilab borar ekan, 1931-yilda Albert-Brauer-Xasse-Nyoter teoremasining shakllantirilishida ishtirok etadi. Ushbu teorema yakuniy o‘lchamliklar algebrasi haqida bo‘lib, nokommutativ algebralar sohasiga taaluqlidir. Oradan atiga ikki yil o‘tib, ya’ni, 1933-yilda Nyoter matematikaga yana bir muhim teoremani — Skolema-Nyoter teoremasini ta’riflab beradi. Biz ushbu teoremalar ta’riflarini ham keltirib o‘tishni lozim topmadik. Chunki, bu teoremalarda juda murakkab mavhum algebraik atamalar va obyektlar qo‘llaniladi va bu teoremalar hozirda faqat soha mutaxassisi bo‘lgan, ya’ni, professional matematiklargagina tushunarlidir.

Murakkab matematik masalalarni ham xamirda qili sug‘urganday oson hal qilib tashlayotgan Emmining ham olima sifatidagi, ham ustoz sifatidagi shuhrati mislsiz ortib ketgan edi. U Gyottingen ko‘chalarida yurganida, orqasida gurillab ergashib yurgan ko‘p sonli talaba-shogirdlarini kuzatish mumkin bo‘lgan. Ba’zan, har qadamda uning ortidan ergashib yuruvchi shogirdlari shu darajada ko‘payib ketardiki, natijada olimaning shogirdlari ko‘chani to‘ldirib yurgan haqiqiy to‘daga aylanardi. Odamlar, ayniqsa Emmining hamkasblari, uni ortidan doim ergashib yuruvchi talabalarni «Nyoter bolalari» deb atashni odat qilishgan. Nyoter bolalari o‘z yoshlariga xos ravishda, juda quvnoq, biroz to‘polonchi, lekin juda zehnli yigit-qizlardan iborat bo‘lgan. Shogirdlar bilan ishlash va o‘z bilganlarini talabalarga ham o‘rgatish amaliyoti Emmining o‘ziga ham juda yoqadigan ish edi. U shogirdlarining har bir yutug‘idan xuddi o‘z muvaffaqiyati singari quvonadigan, fe’li keng, lekin o‘ta talabchan ustoz bo‘lgan. Vaqt o‘tishi bilan Nyoter va Nyoter bolalari shu darajada ahil jamoaga aylanishganki, ular endi shunchaki ustoz-shogird bo‘lmasdan, balki, haqiqatan ham ona-boladek bo‘lib ketishgan. Emmi suzish sportiga qatnagan. Uning suv havzasidagi harakatlari hatto Germaniyaning eng nomdor suzuvchilarini ham qoyil qoldirgan. Olimani yaqindan tanigan ko‘pchilik, uni suzish mashg‘ulotlariga bir to‘da shogirdlari bilan kirib kelganida, «delfin o‘z bolalari bilan keldi« deb ham qo‘yisharkan. U o‘zini qiziqtirayotgan, yoki, shogirdlari muhokama qilayotgan biror dolzarb matematik mavzu bo‘yicha, o‘z «bolalari«, ya’ni, shogirdlari bilan shahar ko‘chalarida yo‘l-yo‘lakay, yoki, biror xiyobon o‘rindiqlarida o‘tirgancha, yoki, hatto, suzish mashqlari davomida ham tinimsiz bahslashishi, munozaralarni olib borishi oddiy hol bo‘lgan. Shogirdlari esa, Emmining o‘zlariga nisbatan ayollarga xos bo‘lmagan tarzda nihoyatda talabchan va qattiqqo‘l bo‘lganligi ishora sifatida, unga kayfiyati yaxshi bo‘lgan vaqtlarda, hazillashib «Der Noether« deb ham murojaat qilishgan. Nemis tilida «der« old qo‘shimchasi faqat erkaklarga nisbatan ishlatiladi. Biroq, Emmiga shogirdlari avvalo uning erkaklardek mardligi, hamda, qattiqqo‘lligini hurmat uchun, samimiy tarzda shunday murojaat qilishgan.

Germaniyada millatchi natsistlar hukumat tepasiga kelgan yillari sodir bo‘lgan bir voqeani mashhur matematik Emil Artinning xotini Natasha Artin-Braunshveyg hikoya qilib bergan. Kunlarning birida Nyoter o‘z «bolalari« bilan Gamburg metrosiga tushadi. Uning barcha shogirdlari har qadamda, shu jumladan metroda ham atrofini o‘rab olib, aytayotgan har bir gapiga quloq solib turishardi. Nyoter esa, deyarli hech qachon matematik mavzulardan boshqa mavzuga o‘tmasdi va shogirdlari bilan ko‘chada piyoda yurganda ham, yoki biror transportda ham albatta muayyan masalani muhokama qilib ketardi. Gamburg metrosida ham shunday bo‘lgan. U vagonda chiqa solib, shogirdlarini atrofiga to‘plagan va ular bilan baland ovozda halqalar nazariyasiga oid matematik masala ustidan suhbat boshlab yuborgan. Emmi odatda mavzuga kirishib ketsa, atrofidagi boshqa narsalarni unutib qo‘yardi. U vagonda boshqa yo‘lovchilarga e’tibor bermay, o‘z «bolalari«ga baland ovozda masalani tushuntira ketgan. Ular metro vagonida muhokama qilayotgan mavzu doirasida esa, mazmuni istisnosiz ravishda faqat va faqat matematikaga taalluqli bo‘lgan, har qanday siyosiy talqinlardan holi atamalar mavjud edi. Xususan, Nyoterning tilidan «ideal«, «fyurer« kabi so‘zlar tez-tez eshitilardi. Garchi, Nyoter siyosatdan yiroq shaxs bo‘lgan bo‘lsa-da, lekin, XX asrning 30-40 yillarida Germaniyada bu jumlalarni ishlatishda juda ehtiyot bo‘lish kerak bo‘lgan. Ular shunchaki matematik atamalarning omonimlari ekanligini hukmron natsistlar politsiyasi — gestapochilarga tushuntirishning imkoni bo‘lmagan. Vagonda yo‘g‘on ovozli, aftidan yahudiyga o‘xshash, atrofiga ham odam to‘plab olgan ayolning xatti-harakatlari albatta hammaning e’tiborini jalb qilgan. Albatta, darhol gestapochilar yetib kelishgan va «ishubhali« shaxslarni tekshirmoqchi bo‘lishgan. Olima va uning shogirdlarini vaziyatdan o‘z o‘quvchilaridan biri olib chiqib ketgan. Olimaning shogirdlaridan biri odatda ataylab gestapo shturm otryadi formasida yurardi. Chunki, bu notinch zamonda faqat shunday niqoblanish bilan o‘z xavfsizligini ta’minlash mumkin bo‘lgan (ya’ni, gestapochilar, o‘zlari kabi formadagi odamga tegishmagan). Niqoblangan ushbu soxta gestapochi «Nyoter bolasi» balki, haqiqiy gestapochilarga vaziyatni nazorat qilib, ushbu to‘da’ni kuzatib kelayotganini tushuntirgan bo‘lsa kerak.

Shu tariqa, Emmi algebraning mumtoz mavzularidan biroz uzoqlashib, o‘z e’tiborini matematikaning aynan bugungi kundagi dolzarb va ilg‘or yo‘nalishlariga qarata boshladi. U ba’zan, Pavel Sergeevich Aleksandrov (1896-1982) bilan birgalikda, topologiya bo‘yicha ham tadqiqotlarga aralashib turardi. Lekin, Emmi Nyoterning matematikadagi mutaxassislik yo‘nalishi — algebraik strukturalarni imkon qadar chuqur va puxta o‘rganishdan iborat bo‘lgan. U, ushbu sohada tekshirilayotgan xususiy hollarni chiqarib tashlab, algebraik strukturalarni iloji boricha umumlashtirilgan holda bayon qilishni maqsad qilgan. 20-yillar oxiri, 30-yillarning boshiga kelib, Emmining matematik sifatidagi nufuzi beqiyos darajada ortib ketdi. Undan ta’lim olish istagida bo‘lgan ming-minglab yoshlar Yevropaning turli burchaklaridan Gyottingenga oqib kela boshlashdi. Emmining shunday xorijiy shogirdlaridan biri Bartel van der Varden (1903-1996) bo‘lib, u keyinchalik bir necha avlod o‘quvchi va talabalar uchun qomusga aylangan «zamonaviy algebra» darsligini yozgan edi (algebrani men ham sahifalari biroz tushunarsiz gotik shrift bilan liq to‘la bo‘lgan ushbu kitobdan o‘rganganman). Van der Varden ustozi Emmi Nyoter haqida shunday yozgan edi:

«Emmi Nyoter uchun sonlar, funksiyalar va matematik amallar orasidagi bog‘liqliklar, ularning muayyan aniq obyektlardan holi ravishda, konseptual mohiyatga keltirilishi orqali, juda sodda va jo‘n tushuniladigan va aniq-tiniq ko‘rinib turadigan darajada bo‘lib qolar edi«.

Albert Eynshteyn esa bunday degandi:

«Nazariy matematika — mantiqan fikrlovchilar uchun o‘ziga xos she’riyatdir. Uning maqsadi — mavjud o‘zaro bog‘liqliklarning maksimal spektrini imkon qadar sodda mantiqiy izchillik bilan, umumlashtirib bayon qilishdan iborat. Mantiqiy go‘zallik yo‘lidagi ushbu jarayonda biz tabiat qonunlarining qa’riga kirib borish imkonini beradigan ajoyib formulalarni kashf qilamiz«.

 

Asosiy algebraik strukturalar

Mavhum algebraning kirish qismiga taalluqli ma’lumotlar keltirilgan ushbu bo‘limni diqqat bilan o‘qib chiqishingizni tavsiya qilamiz. Aks holda, keyingi bo‘limlarda keltiriladigan muhim ma’lumotlarni tushunmay qolishingiz mumkin. Biz esa, o‘z navbatida bu bo‘limni imkon qadar sodda va tushunarli bayon qilishga harakat qilamiz.

Bir yoki, bir necha operatsiyalardan iborat to‘plamlar tarzida qaraladigan asosiy algebraik strukturalarning turi ko‘p. Biz ular ichidan ikkita operatsiya, ya’ni, ○ va Ÿ lar ko‘rib chiqiladigan turlarini qaraymiz. Odatda bu ikkala operatsiyalar + va Ÿ dan iborat bo‘ladi. Ba’zan esa, tashqi kompozitsiyalarning uchinchi qonunini qo‘llash kerak bo‘lib qoladi. Lekin biz, sodda hollarni ko‘rib chiqamiz. Bunda biz, matematika tilidagi «elementidir» so‘zining o‘rniga Î belgisidan foydalanamiz.

Guruh deb, elementlarning A to‘plami va unda aniqlangan ○ operatsiyalarga aytiladi va u quyidagi shartlarni qanoatlantirishi kerak:

1) Istalgan aÎA uchun n ○ a = a ○ n = a bo‘ladigan neytral element n mavjud bo‘ladi;

2) Istalgan aÎA uchun a ○ a⁻¹ = a⁻¹ ○ a = n bo‘ladigan teskari element a⁻¹ mavjud bo‘ladi;

3) Istalgan a, b, cÎA uchun, (a ○ b) ○ c=a ○ (b ○ c) ga muvofiq assotsiaviylik xossasi bajariladi.

Agar, istalgan a, bÎA uchun, biz aniqlagan operatsiya kommutativlik mavjud bo‘lsa, ya’ni, unda a ○ b = b ○ a nisbat bajarilsa, bunday guruhni kommutativ guruh, yoki, abel[1] guruhi deb ataladi.

Agar, guruhda qo‘shish amali (+) aniqlangan bo‘lsa, unda a ga teskari elementni, −a tarzida belgilanadi va uni a ning «qarama-qarshisi» deb nomlanadi. Bu holatda, neytral element 0 bilan belgilanadi.

Agar, guruhda ko‘paytirish amali (Ÿ) mavjud bo‘lsa, unda, a ga teskari elementni 1a 1/a tarzida belgilanadi. Bu holatda, neytral elementni 1 bilan ifodalanadi.

Halqa bu – yana bir Ÿ operatsiyasi mavjud bo‘lgan va assotsiativlik xossasiga ega bo‘lgan kommutativ guruhdir.

4) Istalgan a, b, cÎA uchun a Ÿ (b Ÿ c) = (a Ÿ b) Ÿ c ifoda o‘rinli bo‘ladi.

○ va Ÿ operatsiyalar bir-biri bilan, distirbutivlik xossasiga ko‘ra, quyidagicha o‘zaro bog‘langandir:

5) a Ÿ (b ○ c) = (a Ÿ b) ○ (a Ÿ c)

Halqalarga misol tariqasida natural sonlar ℕ, butun sonlar ℤ, ratsional sonlar ℚ, haqiqiy sonlar ℝ, hamda, kompleks sonlar ℂ ni keltirish mumkin. Ko‘phadlar ham halqa tashkil qiladi. Halqalar sohasida ○ operatsiyasi (amali), xuddi ko‘paytirish amali singari, kommutativlik xossasiga ega bo‘ladi va shuning uchun ham uni + belgisi bilan belgilanadi. Ÿ operatsiyasi (amali) esa, xuddi ko‘paytirish amali singari ∙ bilan belgilanadi (tushunarli bo‘lishi uchun, buni ham kommutativlikka ega deb olamiz).

Agar ixtiyoriy A qism to‘plam ○ va Ÿ amallarni shu to‘plamda chegaralaganda guruh yoki halqa bo‘lib qolaversa, unda bunday A qism to‘plamni qism guruh, yoki, qism halqa deb ataladi. Ideal esa – halqaga oid alohida tushuncha bo‘lib, u shunday BÌA halqa osti halqasiki, unda, istalgan bÎB va B ga tegishli, yoki tegishli bo‘lmagan boshqa istalgan elementning ko‘paytmasi ham albatta B ga tegishli bo‘ladi. Ideallarni qo‘shish va ko‘paytirish mumkin. Ideallarni qo‘shish va ko‘paytirishning natijasi ham albatta ideal bo‘ladi. Ideal tushunchasi aslida, son tushunchasini umumlashtirish orqali paydo bo‘lgan. Ikkita I va J ideallar uchun:

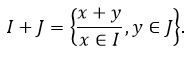
Norvegiyalik mashhur matematik Nils Xenrik Abel sharafiga shunday nomlagan.

ga egamiz. IJ ni aniqlash biroz murakkab jarayon. Bu ideal,  xÎI, yÎJ bo‘yicha, barcha xy ko‘paytmalardan kelib chiqqan. Shunga o‘xshash ko‘paytmalarga ega bo‘lgan har qanday turdagi ideallarning kesishishi natijaviy ideal deyiladi.

Butunlik sohasi deb, ∙ amali uchun nolga bo‘linuvchilarga ega bo‘lmagan A halqaga aytiladi. Boshqacha aytganda, bunday halqada b∙a=a∙b=0 shartga mos keluvchi a va b elementlar mavjud bo‘lmaydi.

Bunday holda esa, A halqa kommutativ halqa bo‘ladi va unda birlik elementi mavjud bo‘ladi; ya’ni, ∙ operatsiyasi uchun birlik vazifasini bajaruvchi neytral element aniqlangan bo‘ladi:

a∙1=a.

Endi, butunlik sohasini 0 siz qarab chiqamiz. Uni A*=A|{0) tarzida belgilaymiz. Agar, ∙ operatsiyasi A* uchun kommutativ guruhni aniqlasa, unda, A ni biz maydon deb ataymiz. Agar, A* kommutativ bo‘lmasa, unda biz A ni jism deb ataymiz. Bunday murakkab ta’riflar va tushuntirishlarda cho‘chishga hojat yo‘q: agar A halqa tugal chekli bo‘lsa, unda, mashhur Vedderbyoner teoremasiga ko‘ra, ushbu halqa albatta kommutativ bo‘ladi. Agar, A halqa cheksiz bo‘lsa, unda, algebrachilar uchun erkinlik yuzaga keladi.

Zamonaviy algebraik olamning noyob turlaridan bo‘lmish A-modullarni ko‘rib chiqamiz. Chapki A-modulni aniqlash uchun, birlikka ega bo‘lgan A halqa va kommutativlikka ega bo‘lgan M guruh kerak bo‘ladi. a, b Î A va M(m, n Î A) elementlar ustida amallar, odatiy tarzda quyidagicha aniqlanadi:

1) (ab)m=a(bm);

2) (a+b)m=am+bm;

3) a (m+n)=am+an;

4) 1m=m.

Xuddi shunday tarzda, o‘ng A-modul ham aniqlanadi; kommutativ modul, (yoki, shunchaki A-modul) bu – bir vaqtning o‘zida ham chapki va ham o‘nggi bo‘ladigan moduldir. Agar, A – maydon bo‘lsa, unda, A-modul vektor fazo deyiladi.

Agar vektor fazoning vektorlari uchun ko‘paytirish amali aniqlangan bo‘lsa, demak, unda biz «algebra»ga ega bo‘lamiz.

 

Keling, gapni shu joyda to‘xtataylik. Garchi, biz yuqorida keltirgan ta’rif va tushunchalar matematikada elementar oddiy tushunchalar sanalsa-da, lekin kitobxon uchun ular oddiy va tushunarli bo‘lishi qiyin…

Algebra, ideal va Nyoter halqalari haqida ikki og‘iz

Emmi Nyoter ilmiy faoliyatining katta qismi algebraik strukturalar – halqalar va ideallarga bag‘ishlangan. Nyoter nima sababdan bu mavzularga shu qadar jiddiy e’tibor qaratgan ekan?

Matematiklar ish olib boradigan ko‘plab obyektlar aslida halqalardir: masalan, butun sonlar to‘plami ℤ va uning keyingi kengayib borishi — ℚ, ℝ va ℂ lar ham halqalardir. Shuningdek, koeffitsiyentlari yuqorida qayd etib o‘tilgan halqalardan iborat bir o‘zgaruvchili ℤ[X], ℚ[X], ℝ[X], va ℂ[X] ko‘phadlar ham halqalar sanaladi. Shunga o‘xshash, bir necha o‘zgaruvchilarning ko‘phadlari ℤ[X₁, X₁, …, X_n ], ℚ[X₁, X₁, …, X_n ], ℝ [X₁, X₁, …, X_n ], va ℂ[X₁, X₁, …, X_n ] lar ham halqalardir. Bundan tashqari, tutash qatorlar va yana boshqa ko‘plab matematik obyektlarni halqalar sifatida qarash mumkin.

Lekin, ideallar nima va ular nima sababdan bunday ajoyib nomga ega bo‘lishgan? Keling, shu o‘rinda matematika tarixiga kichik bir ekskursiya uyushtiramiz. Misol tariqasida kvadratik butun son ℤ[√− ⁵] yoki, shunga o‘xshash bo‘lgan, ℤ[i√− ⁵] ni ko‘rib chiqamiz. Bu: a+b ko‘rinishdagi sonlar to‘plamidir va bu o‘rinda a va b – butun sonlar bo‘ladi. Boshqacha aytganda:

 

ℤ[√− ⁵] bu – halqadir. Lekin, bu o‘rinda, agar biz matematika tili bilan aytsak, «ta’qiqlangan hudud»ga qadam bosmoqdamiz. Biz bo‘linishning standart xossalariga ko‘nikib qolganmiz va boz ustiga, sonning umumiy ko‘paytuvchilari odatda ushbu son uchun yagona umumiy ko‘paytuvchilar bo‘lishadi. Masalan, 21 sonini qaraydigan bo‘lsak: 21=3∙7 umumiy ko‘paytuvchilarga ega bo‘ladi va ular 21 uchun yagonadirlar. Ya’ni, 21 ni faqat 3 va 7 ga bo‘lish mumkin xolos. Ushbu tasdiq arifmetikaning asosiy teoremasidan kelib chiqadi: ℤ to‘plamda sonni oddiy ko‘paytuvchilarga ajratilsa, ular mazkur son uchun yagona bo‘ladi. ℤ [√− ⁵] to‘plamda esa ushbu tasdiq o‘z kuchini yo‘qotadi. Bu o‘rinda biz, 21 ni oddiy ko‘paytuvchilarga ikki xil yo‘l bilan ajratishimiz mumkin bo‘ladi:

3·7=(4+√−5) (4−√−5)=21

3∙7=4+-54--5=21

Ushbu to‘plamda sonni oddiy ko‘paytuvchilarga ajratish endilikda yagonalik xossasiga ega bo‘lmaydi. Ya’ni, uning ko‘paytuvchilari faqat bitta juftlikdan iborat bo‘lmaydi. Ushbu g‘alati xulosaga birinchi bo‘lib Ernst Kummer (1810-1893) kelgan edi. Bir qarashda unchalik ham muhim bo‘lmagan va atiga bir satr yozuv bilan ifodalanadigan ushbu tasdiq, XIX asr algebrachilari uchun Ferma teoremasini isbotlash yo‘lida jiddiy g‘ov bo‘lgan va ko‘plab boshqa noqulayliklar paydo qilgan edi.

Vaziyatga oydinlik kiritish va muammoga qandaydir yo‘sinda yechim topish maqsadida Kummer ideal sonlar tushunchasini fanga joriy qildi. Biroq, Kummerning ideal sonlari o‘zi o‘ylagandek foydali bo‘lib chiqmadi. Chunki ular ℤ[√− ⁵] ga emas, balki, boshqa, yanada katta halqaga tegishli edi.

Aslini olganda, Kummer ideallarini son ham deb bo‘lmaydi. Ularni bugungi kunda biz o‘zaro ekvivalent bo‘lgan sonlar to‘plami deb nomlagan bo‘lar edik. O‘sha zamon matematiklari uchun hozirgidek umumqabul qilingan faktor-to‘plam va gommomorfizm tushunchalari ma’lum emas edi. Ideallar olamiga qandaydir mantiq va tartibni faqat Rixard Dedekind (1831-1916) olib kirgan. Uning ortidan esa, boshqa algebraistlar ham ergashishgan va ideallar bo‘yicha tadqiqotlarni quloch yozdirib yuborishgan. Ideallar matematikasi sohasida shunday avlod vakillaridan biri – Emmi Nyoter edi.

Ideallarning yana bir ajoyib xususiyati mavjud. Bu o‘rinda ideallarning zanjirlari haqida gap bormoqda. Biz Nyoterning bu borada bajargan ishlarini bayon qilib o‘tirmaymiz va mavhum tushunchalarni izohlashga harakat qilmaymiz. Buning o‘rniga juda oddiy bir misol keltirish bilan cheklanamiz: ideallar – butun sonlar bo‘lmish ℤ halqalaridir.

Ideallar olamida arifmetikaning asosiy teoremasi hukmronlik qiladi. Ideal aslida butun sonlar sohasini o‘zida namoyon qiladi, ya’ni, uni «yaxshi halqa» deyish mumkin. bunda, haqidagi hamma sonlar uchun sonni oddiy ko‘paytuvchilarga ajratishda yagonalik saqlanadi va bunday izchillikni hech narsa buzmaydi. Bunda n ga karrali bo‘lgan butun sonlardan iborat nℤ to‘plam ideallarni tashkil qiladi. Bunday ideallarning miqdori, xuddi sonlarning o‘zi singari cheksiz bo‘ladi. ideallarning yig‘indisi va ko‘paytmasi esa juda oson topilishi mumkin:

aℤ+bℤ=(a+b)ℤ
aℤ∙bℤ=abℤ

Mohiyatan sonlar to‘plami bo‘lmish ideallar, hamda oddiy sonlarning o‘zini tutishi bir xil bo‘ladi; ular ko‘paytuvchilarga ham bir xil ajratiladi va arifmetika nuqtai nazaridan ham ekvivalent bo‘ladi. Ular shuningdek bo‘linish singari murakkab sohada ham o‘zaro ekvivalent bo‘lishadi. Aslida, ideallar uchun «b son a» ga bo‘linadi tasdig‘ini bℤÌaℤ tarzida ifodalash mumkin. Nyoterning eng dohiyona yechimi shunda ediki, u tegishlilik funksiyasi Ì orqali birlashtirilgan ideallar zanjirini, ularning bo‘linish belgisini yaqqol ifodalaydigan qilib tartiblay olgan.

Istalgan nisbatdagi bo‘linish amali ertami-kechmi, baribir qachondir albatta muayyan bir son bilan yakunlangani uchun, ideallar zanjiri ham xuddi shunday, ertami-kechmi, baribir tugaydi. Ideallarning «yaxshi» zanjirlari albatta yakunlanadi, ya’ni u tugal cheklangan bo‘ladi. Ideallarning cheksiz zanjirlari mavjud bo‘lmagan halqalarni Nyoter halqalari deyiladi. O‘z tadqiqotlarida Emmi Nyoter aynan shunday halqalarga juda katta e’tibor qaratgan.

Keyinchalik, algebrachilar quyidagi tasdiqlarning ham haqligini isbotlashdi:

1) A halqa nyoter halqasi bo‘ladi (boshqacha aytganda, undagi ideal zanjirlarining o‘sib boruvchi miqdori cheklangandir).

2) Istalgan ideal A ga ko‘ra tugal chekli bo‘ladi.

3) Ideallarning istalgan to‘plamida A ga ko‘ra eng katta ideal mavjud bo‘ladi.

1999-yilda Avstraliya matematika fondi 18ℤ ideal uchun ℤ to‘plamning o‘suvchi zanjirlari tasviri tushirilgan futbolkalarni sotuvga chiqardi. Futbolkaga boshqa misol tasvirini tushirish uchun esa, futbolkalarning o‘lchamlari chekli ekanligi xalaqit qilgan. O‘sha liboslarda quyidagi ideallar zanjirlarini ko‘rish mumkin edi:

18ℤÌ9ℤÌ3ℤÌℤ
18ℤÌ6ℤÌ3ℤÌℤ
18ℤÌ6ℤÌ2ℤÌℤ
18ℤÌ9ℤÌℤ
18ℤÌ6ℤÌℤ
18ℤÌ3ℤÌℤ
18ℤÌ2ℤÌℤ
18ℤÌℤ

Kutilganidek, ushbu zanjirlar tugal cheklidirlar. ℤ halqa esa nyoter halqasidir. Gilbert, agar muayyan A halqa nyoter halqasi bo‘lsa, unda, A[X] ko‘phadlar halqasi ham nyoter halqasi bo‘lishini isbotlab bergan.

Yakun

1930-yillar oxiriga kelib, jahon matematiklari orasida Emmi Nyoterning obro‘si mislsiz oshib ketgan edi. Uni 1932-yilda o‘tkazilgan Xalqaro kongressda eng nufuzli mehmonlardan biri sifatida kutib olishgan. Keyingi, ya’ni, 1933-yilda Nyoterning ona vatani — Germaniyada nihoyatda xunuk ishlar bo‘lib o‘tdi. Muayyan xatti-harakatlardan keyin hukumatni o‘ta keskin millatchilik kayfiyatidagi natsistlar to‘dasi egallab oldi. Ularning ahmoqona qarorlarini va johilliklari, nemis xalqi boshiga eng manfur kunlarni sola boshladi. Chunonchi, natsistlar mamlakatdagi barcha universitet va maktablarda ishlayotgan yahudiy o‘qituvchilarni ishdan haydalishini talab qila boshlashdi. Antisemitizm deb nomlangan ushbu ahmoqona harakat tufayli Emmi Nyoter ham jabr ko‘rdi. Millatchilik kayfiyatidagi hukumatning bunday be’mani ishlariga norozilik bildirgan nemis ziyolilari ham ta’qibga olina boshladi. Yahudiy hamkasblarining huquqlari uchun kurashmoqchi bo‘lgan nemis olimlari deyarli xoinga chiqarib qo‘yilardi. Shunday murakkab va tahlikali sharoitda, aslida Germaniya ilm-fanida muhim vazifalarni egallab kelgan ko‘plab yahudiy olimlari, xususan, Albert Eynshteyn, Tomas Mann, Stefan Tsveyg, Zigmund Freyd, Maks Born kabilar, o‘z o‘qituvchilik faoliyatlarini to‘xtatishlariga to‘g‘ri keldi. Tez orada esa, natsistlar tomonidan yahudiy olimlarning hayoti uchun ochiqchasiga tahdid qilina boshlandi. Qandayin nufuzga ega bo‘lmasin va ilm-fan uchun qanaqa ulkan xizmatlar qilgan bo‘lmasin, endilikda yahudiy olimlari shunchaki yahudiyligi uchun sudsiz-so‘roqsiz o‘ldirib yuborila boshladi. Natijada, ushbu millatga mansub olimlar zudlik bilan bexatar yerlarga qochishga kirishishgan. Shunda ham, ulgurgan ulgurdi. Qochishga ulgurmaganlar esa, yoki natsistlarning g‘ayriinsoniy sharoitlardagi mehnat lagerlarida ochdan o‘lgan, yoki, shunchaki otib tashlangan. Balki insoniyat natsistlarning ilm-fanga, xususan, algebraga yetkazgan zarari miqyosini endi hech qachon bila olmas.

Barcha yahudiylar kabi, bunday tahlikali sharoitda Emmi Nyoter ham biror xavfsiz joyga qochib jonini saqlashi zarur edi. Uning akasi Frits sovet ittifoqiga — Tomsk shahriga yo‘l oldi. Emmi esa, bir muddatgacha Moskvaga yoki, Oksfordga ko‘chib o‘tish borasida ikkilanib yurdi (u g‘oyaviy jihatdan kommunistik tuzumga xayrixoh bo‘lgan). Biroq, shunday ulkan salohiyatli matematik olimani o‘z ilmiy jamiyatlariga qo‘shib olish borasida sovetlar ham, britanlar ham sustkashlik qilishdi. Uloqni esa okean ortidagilar ilib ketishgan. Multimillioner Rokfeller fondining sayi-harakatlari evaziga AQSH olimlari Emmi Nyoterni o‘z mamlakatlariga ko‘chib kelib ishlashga ko‘ndirishga muvaffaq bo‘lishgan. o‘rni kelganda aytish kerakki, ikkinchi jahon urushi arafasi sanaladigan o‘sha — 30 yillar oxirlariga kelib, Germaniyadagi antisemitizm kayfiyati okean ortidagi ayrim muassasalarda ham kurtak yoza boshlagan bo‘lib, masalan, Nyu-Jersidagi Prinston universitetida ham yahudiy o‘qituvchi va talabalarga nisbatan turli adolatsizliklar avj ola boshlagandi. Shu sababli, badavlat yahudiy oilalari o‘z millatlariga mansub o‘qituvchilar va ayniqsa, talabalar uchun yaxshiroq sharoitlar hozirlash maqsadida, boshqa, nisbatan sog‘lom muhit hukmron bo‘lgan oliygohlar uchun homiylik mablag‘lari ajrata boshlashgan. Misol uchun, xayriya ishlarida doimo o‘rnak ko‘rsatuvchi Bambergerlar oilasi Prinstonning o‘zidagi boshqa bir oliygoh — Prinston istiqbolli tadqiqotlar Instituti uchun bir necha million dollar miqdorida mablag‘ ajratishgan. Ushbu yirik xayriya mablag‘lari evazida mazkur institut ko‘plab nufuzli olimlarni va istiqbolli yosh tadqiqotchilarni o‘ziga jalb qila boshladi va tez orada butun AQSHda dong‘i ketgan yetakchi institutlardan biriga aylandi. Ushbu institutning eng muhim jihati shu ediki, bu yerda olimlar faqat ilmiy tadqiqotlar bilan shug‘ullanib, butun diqqat-e’tiborlarning to‘laligicha o‘rganilayotgan mavzuga qaratishgan. Hech kim ularni bir vaqtning o‘zida talabalarga ham dars berishga majburlamagan. Maosh ham faqatgina ilmiy tadqiqot uchun to‘langan. Shu tarzda, bu dargoh ko‘plab olimlar va izlanuvchilar uchun erkin ishlash imkonini beradigan bog‘i eramga aylangan desak mubolag‘a bo‘lmaydi. o‘sha yillarda Germaniyada va bir qator qo‘shni oliygohlarda avj olgan antisemitizm kayfiyati tufayli jabr ko‘rgan yahudiy millatiga mansub olimlar uchun esa, Prinston istiqbolli tadqiqotlar Instituti ham ish joyi, ham boshpanaga aylangan. Germaniyadan AQSHga qochib kelib, mazkur institutda qo‘nim topgan yahudiy olimlari orasida Albert Eynshteyn, German Veyl, Jon fon Neyman, hamda Kurt Gyodel singari eng yorqin ilm yulduzlarini uchratish mumkin edi. Ular qatorida Prinstonga bizning qahramonimiz Emmi Nyoter ham yetib kelgan. Bungacha u Rokfeller fondi taqdim etgan grant asosida Pensilvaniyaning Brin-Mor shahrida joylashgan, ayollar uchun ixtisoslashtirilgan Brin-Mor kollejida matematikadan dars bergan edi. Prinstonga yetib kelgan Emmiga ushbu institutda ma’ruzalar qilish va seminarlar o‘tkazish imkoni berilgan bo‘lsa-da, lekin uni ushbu institutga to‘laqonli ishlash uchun qabul qilishmagan va o‘qigan ma’ruzalari yoki seminarlari uchun haq to‘lashmagan. Sababi esa yana o‘sha eski gap: qanchalik kuchli matematik olima bo‘lmasin, u shunchaki ayol kishi edi. Shu sababli, u baribir qo‘shni Brin-Mor kollejida ishlashni ham tashlab qo‘ya olmasdi. Emmi nima bo‘lgan ham matematikani hech qachon tashlab qo‘ymasdi va bo‘sh vaqt bo‘ldi deguncha, o‘zini qiziqtirayotgan biror masala yuzasidan izlanishga tushib ketardi. U avvalgidek, mavzuni hamkasblari bilan muhokama qilishni yoqtirardi. Emmi mavzuga berilib, kirishib ketgan paytlarda esa, allaqachon Amerikada ekanligini ham unutib qo‘yib, atrofidagilarga sof nemis tilida gap uqtirishga urinib qolardi. Shunday munozaralar esa, odatda ishtirokchilar uchun ham, tinglovchi-tomoshabinlar uchun ham faqat koni foyda bo‘lgan. Hatto ba’zi talabalar shunchaki Emmining ilmiy bahslarini eshitish va imkon bo‘lsa yozib olish uchun uning eshigini poylashardi.

Amerikaga ko‘chib o‘tganiga va biroz erkin hayot boshlaganiga atiga ikki yil bo‘lgan paytda, vrachlar Emmi Nyoterga bachadon saratoni xastaligi tashxisini qo‘yishdi. Jismonan baquvvat bo‘lgan olima jarrohlik amaliyotidan juda yaxshi o‘tgan. Biroq, vrachlar Emmining juda tez oyoqqa turib ketishiga umid bog‘lab turgan bir vaqtda, olima operatsiyadan keyingi to‘rtinchi kuni emboliya tufayli jon bergan. Vafot etgan paytda olima 53 yoshda edi.

Emmi Nyoterning vafoti haqidagi qayg‘uli xabar butun matematika olamini motamga solgan. Olimaga bag‘ishlab yozilgan marsiya hatto natsistlar Germaniyasida ham chop etilgan. Van der Varden muallifligida chop etilgan ta’ziyanomani esa natsist taqrizchilari shunchaki algebraga tushunmaganlari uchun «o‘tkazib« yuborishgan deyish mumkin. Sababi unda muallif asosan Emmi Nyoterning matematikaga qo‘shgan xossasini alqab, maqola matnini ko‘proq matematik atama formulalar bilan to‘ldirgan (balki, natsist senzorning matematikaga toqati bo‘lmagandir).

Emmi Nyoter Brin-Mordagi Keri Tomas kutubxonasi devorlari ostiga dafn qilingan. Hozirda olimaning sharafiga Oyning teskari tarafidagi kraterlardan biri, hamda, 1955 yilda kashf qilingan 7001 raqamli asteroid[1] uning nomi bilan ataladi.

 

Nyoter va shaxmatchi teoremasi

Yetuk matematik, algebrachi Emmanuil Lasker (1868-1941) bir vaqtning o‘zida shaxmat bo‘yicha jahon chempioni sifatida ham mashhur bo‘lgan. U oddiy, sodda vaprimar ideallar yuzasidan mufassal izlanishlar olib borgan. Mavhum algebraga chuqur ketmaymiz-da, keling, o‘zida butunlik sohasini ham namoyon qiluvchi A halqani ko‘rib chiqamiz. Ushbu halqada primar ideal deb, boshlang‘ich A halqadan farqli bo‘lgan shunday i idealga aytiladiki, unda,abÎi va aÏi bo‘lganda bnÎi bo‘ladigan biror n mavjud bo‘ladi. (n=1 da bu ideal oddiy ideal deyiladi). Lasker halqalar bo‘yicha juda keng doirali ilmiy ishlar qilgan va o‘z nomi bilan ataluvchi, ya’ni, «Lasker halqalari» sohasini mufassal bayon qilgan. Lasker halqalari ideallarning juda qiziq bir xossasiga asoslanadi. Ya’ni u, istalgan idealni muayyan sondagi primar ideallarning kesishmasi sifatida qarash mumkinligiga tayanadi.

Emmi Nyoter hozirda Lasker-Nyoter teoremasi deb yuritiladigan teoremani isbotlashga muvaffaq bo‘lgan. Mazkur teorema quyidagicha ta’riflanadi:

«Butunlikning istalgan nyoter sohasi Lasker halqasi bo‘ladi«

Mavhum algebra sohasiga mansub bo‘lgan ushbu teorema, bir qarashda bir-biridan juda yiroq bo‘lgan ikki xil matematik tushunchalarni, ya’ni, ideallarning chekli zanjiri hamda, primar ideallarning kesishmalarini o‘zaro uyg‘unlashtiradi.

Matematika bilan yaqindan tanish bo‘lgan kitobxon allaqachon sezgan bo‘lsa kerak: agar biz Nyoter-Lasker teoremasini ? halqaga tadbiq qilsak, unda arifmetikaning asosiy teoremasini keltirib chiqaramiz: istalgan sonni, bitta va faqat bitta usul bilan, oddiy ko‘paytuvchilarning ko‘paytmasi sifatida tasavvur qilish mumkin. Hozirda matematiklar keng qo‘llaydigan «nyoter halqasi» atamasini, Burbaki guruhi asoschilaridan biri bo‘lmish mashhur fransuz matematigi Klod Shevelle (1909-1984) fanga joriy etgan.

 

 

---

[1] (7001)Noether asteroidi

---

[1] Norvegiyalik mashhur matematik Nils Xenrik Abel sharafiga shunday nomlagan.

---