Ajoyib kvadratlar

Afsonalarg ko‘ra, ajoyib kvadratlar o‘yinini qadimgi Xitoyda o‘ylab topishgan ekan. Ushbu g‘oyat qiziq matematik o‘ying bag‘ishlangan ilk qo‘lyozm ma’lumotlar esa, eramizdan avvalgi 2200-yillarg taalluqli bo‘lib, Imperator Yu zamonasidagi shunday kvadratlar haqid so‘z yuritadi. Ajoyib kvadrat N² sondagi kataklardan iborat bo‘lib, kataklarning har biriga, boshqasida takrorlanmaydigan butun sonlar yozilgan. Sonlarning kataklarda joylashuv tartibi shunday bo‘lishi kerakki, ularni istalgan yo‘nalishda — xoh gorizontal, xoh vertikal v xoh diagonal yo‘nalishda qo‘shib chiqilsa, barch taraflarda yig‘indi bir xil chiqishi kerak.

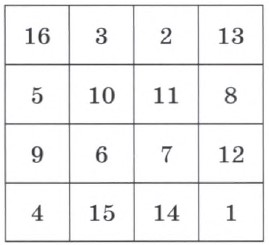
Agar, ajoyib kvadratdagi barch butun sonlar to‘plami 1 dan N² gach bo‘lgan ketma-ketlik qatorini tashkil qilsa, unda, ushbu ajoyib kvadratni N-tartibli kvadrat deyiladi. Bunday kvadratdagi hamm yo‘nalishd bir xil chiqadigan yig‘indini es «sehrli son» deyiladi v u konstant bo‘ladi. Mazkur «sehrli son» istalgan ajoyib kvadrat uchun doimo N(N²+1) g teng bo‘ladi. Uyg‘onish davri musavviri bo‘lmish Albrext Dyurer 1514-yild ushbu ajoyib kvadratni tuzib, ommag namoyish qilgan edi. Uning o‘lchami 4×4 ko‘rinishda.

E’tibor bersangiz, eng quyi qatordagi ikkinchi v uchinchi kataklardagi (ikkit markaziy katakdagi) sonlar o‘zaro ulab yozilsa «1514» raqami hosil bo‘ladi. Ya’ni, musavvir shu tariqa, ushbu ajoyib kvadratning hosil qilingan yilini ham kvadratning o‘zig mohirona tarzda muhrlab qo‘ygan. Albrext Dyurerning ushbu ajoyib kvadratida barcha satrlarning ham diagonal, ham gorizontal va ham vertikal yo‘nalishlar bo‘yicha yig‘indisi 34 ga teng chiqadi. Boz ustiga, ushbu ajoyib kvadratning eng chetki, ya’ni, burchaklardagi kataklarida joylashgan to‘rtt sonning yig‘indisi ham 34 ga teng chiqishidan tashqari, markazdagi kichik kvadratdagi to‘rtta katakdagi sonlar yig‘indisi ham 34 g teng chiqadi!

Ushbu singari ajoyib kvadratlarni chuqur tadqiq qilgan yetuk matematik Bernar Frenikl de Bessi bo‘lib, u 1602-1675 yillar orasida Fransiyad yashab o‘tgan. De Bessi to‘rtinchi tartibli ajoyib kvadratlarning bo‘lishi mumkin bo‘lgan barcha variantlarini aniqlagan va ularning yechimlarini ko‘rsatgan. To‘rtinchi tartibli ajoyib kvadratlarning jami soni 880 tani tashkil qiladi va ularning barchasi, de Bessining o‘limidan so‘ng chop etilgan kitobi — «Ajoyib kvadratlar vaa jadvallar haqida» nomli asarid keltirib o‘tilgan. De Bessi haqli ravishda, bugungi kunda ham ajoyib kvadratlar qiroli hisoblanadi.

Odamzot 3×3 o‘lchamdagi eng sodda ajoyib kvadratlarni o‘ylab topganidan beri ancha muddat o‘tdi. Qizig‘i shundaki, 3×3 o‘lchamdagi eng sodd ajoyib kvadratlar, bir qarashda bir-biri bilan umuman aloqada bo‘lmagan, mutlaqo o‘zaro yot sivilizatsiyalarda ham qadimdan ma’lum bo‘lgan. Xususan, shunday ajoyib kvadratlar Mayya hindularida ham, Afrikadagi Xasus qabilasid ham, Janubiy-Sharqiy osiyo changalzorlarida yashagan xalqlarda ham bo‘lgan. Hozirda matematiklar yuqori o‘lchamlikdagi fazoviy jismlar sirtidagi ajoyib kvadratlarning xossalarini o‘rganishmoqda. Xususan, to‘rt o‘lchamli giperkub bo‘ylab, barch yo‘nalishlarda teng yig‘indi keltirib chiqaruvchi ajoyib kvadratlar o‘rganilmoqda.

Rasmda: Barselonadagi nasroniylar ibodatxonasid 4×4 o‘lchamdagi ajoyib kvadrat tasviri tushirilgan bo‘lib, u barch yo‘nalishlar bo‘yich yig‘indid 33 raqamini beradi. Ularning e’tiqodig ko‘ra, ushbu raqam Iso Masiyhning samog ko‘tarilgan paytidagi yoshini ifodalar emish. Lekin, ushbu kvadratni asl ajoyib kvadrat deyish ham to‘g‘ri emas. Chunki, bund shart bajarilmayapti. Ya’ni, kvadrat ichidagi kataklard ba’zi sonlar takrorlanmoqda.

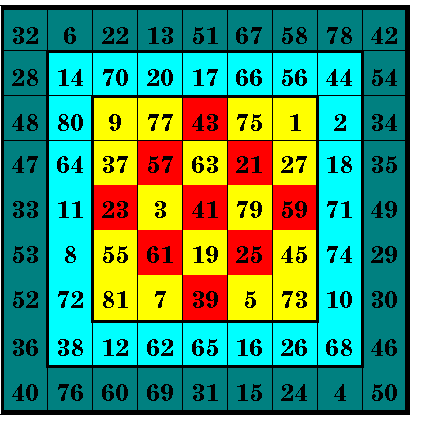
Ajoyib kvadratlar haqida gap ketgand Jon Xendrik tuzgan eng murakkab va shu bilan birg eng mukammal ajoyib kombinatsion kvadratni ham esga olib o’tish shart. Jon Xendrik ajoyib kvadrati 9-tartibli ajoyib kvadrat bo’lib, und 1 dan 81 gacha bo’lgan sonlar ishtirok etadi. Unda hamma yo’nalishlar yig’indi bo’yicha 369 raqamig teng bo’lib chiqadi. Shu bilan birga, ushbu kvadrat ichid yana ucht boshqa ajoyib kvadratlar ham shunday mohirona joylanganki, ularning o’zida ham 287, 205 v 123 sonlari chiqadi. Ushbu ichki ajoyib kvadratlar moviy, sariq va qizil ranglar bilan alohida yaqqol ko’rsatilgan. Qizil rangli, ya’ni 3-tartibli markaziy ichki ajoyib kvadrat 45° ga burilgan holda tasvirlangan.

Umuman olganda, agar ajoyib kvadratlar mavzusiga qiziqsangiz ushbu saytdan yanada ko’proq ma’lumot olishngiz mumkin (sayt ingliz tilida): http://www.magic-squares.net/magic_squares_index.htm

Bizni ijtimoiy tarmoqlard ham kuzatib boring: