15 o‘yini yoki Taken

(Mumtoz matematik maqolalar turkumidan)

 

Ya.I.Perelmanning «Qiziqarli matematika« (1938) kitobidan tarjima.

 

Raqamlangan 15 ta kvadrat shashka teriladigan qutichaning qiziq tarixi borligini ko‘pchilik bilmasa kerak. Bu haqida, tarixchi-tadqiqotchi V.Arens so‘zi bilan hikoya qilamiz.

XIX asrning 70-yillarida, AQSHda «15« o‘yini paydo bo‘ldi; u tez tarqaldi va bu o‘yin ishqibozlari hisobsiz darajada ko‘payib ketganligidan, u chinakam ijtimoiy ofatga aylandi.

Okeanning berigi tarafida, ya’ni Yevropada ham ahvol shunday edi. Bu yerda ko‘nkalarda (ot qo‘shilgan aravadan iborat yo‘lovchi tashuvchi shahar ichi temir yo‘l transporti, tramvayning ajdodi) ham yo‘lovchilar qo‘lida 15 ta shashkali qutichalarni ko‘rish mumkin edi. Idoralarda va do‘konlarda xo‘jayinlar o‘z xizmatchilarining o‘yinga berilib ketib, ishni tashlab qo‘yganliklari sababidan g‘azablanib, ish va savdo vaqtida bu o‘yinni o‘ynashni ta’qiqlab qo‘ydilar. o‘yin-kulgi muassasalarining egalari, odamlarning bu o‘yinga bo‘lgan katta qiziqishdan foydalanib, yirik turnirlar uyushtirar edilar.

o‘yin hatto Germaniya Reyxstagining muhtasham zallariga ham kirib bordi. Reyxstagda oppoq sochli mo‘ysafidlarning o‘z qo‘llaridagi kvadrat qutichaga termulib o‘tirganlarini hali ham ko‘z oldimdan ketmaydi« — deydi o‘sha vaqtlarda Reyxstag deputati bo‘lgan mashhur geograf va matematik Zigmund Gyunter.

 

«Parijda bu o‘yin ochiq maydonlarda, xiyobonlarda ham o‘ynaladigan bo‘lib qoldi. Tez fursatda poytaxtdan butun chekka joylarga tarqaldi. Qishloqlarda bu o‘rgimchak to‘ri kirib bormagan uy deyarli yo‘q edi; u hamma joyda o‘z o‘ljalarini tuzoqqa ilintirib olish payida edi« — deb yozgan edi bir farang yozuvchisi.

1880-yil 15-o‘yinining vasvasasi eng avjiga chiqqan yil bo‘lsa kerak. Biroq shundan keyin, matematika quroli bu zo‘ravonni shikastladi va mag‘lub etdi. o‘yinning matematik nazariyasi shuni fosh qilib berdiki, taklif etilishi mumkin bo‘lgan juda ko‘p masalalardan faqat yarminigina yechsa bo‘lar ekan. Ikkinchi yarmini esa, har qanday hiyla-nayrang bilan ham yechib bo‘lmas ekan.

Matematik isbotlashlar orqali, nima uchun ba’zi masalalari har qancha zo‘r berish bilan ham yechib bo‘lmasligi ochib berildi. Nima uchun bunday o‘yinlarni uyushtiruvchilarning masalalarni yechishga katta-katta pullar va’da qilishda botirlik ko‘rsatayotganliklari sababi ochilib qoldi. Bu xususda o‘yin ixtirochisining o‘zi hammadan o‘tib tushdi: u Nyu-Yorkdagi nufuzli bir gazetaning muharririga, gazetaning yakshanba soni ilovasida 15 o‘yiniga oid (yechimi yo‘q, yechib bo‘lmaydigan variantdagi) masalani bosib chiqarishni va uni yechgan kishiga 1000 dollar mukofot va’da qilishni taklif qilgan; muharrir ikkilanganligi sababli, ixtirochi aytilgan mablag‘ni o‘z yonidan to‘lashga tayyor ekanligini bildirgan. Ixtirochining ismi Samuel LLoyd bo‘lib, uni Sem Lloyd deb atashardi. Sem Lloyd xilma-xil jumboqlar va ajoyib matematik masalalarni o‘ylab topish bilan katta shuhrat qozongan edi. Shunisi qiziki, u o‘zi o‘ylab topgan 15 o‘yiniga AQSH patent idorasidan patent ola olmagan. Yo‘riqnomaga muvofiq, patent idorasi amaldori, Sem LLoyddan ixtironing «ishchi modeli«ni olib kelib namoyish qilishini talab qilgan. Sem Lloyd talabga muvofiq o‘yinni keltirib, amaldorga taqdim qilgan. Amaldor o‘yinning masalasini yecha olmagan, ya’ni 15 ta kvadrat shashkani tartiblay olmagan. Unga masalaning yechimi yo‘q xili berilgan ekan. Shu sababli, patent idorasi mansabdor shaxsi, o‘yinni yechib bo‘lmas ekan, demak u ishchi model hisoblanmaydi degan izoh bilan patent berishni rad qilgan. Lloyd bu xulosaga qanoatlanib qo‘ya qolgan, chunki u o‘z ixtirosining bu qadar shuhrat qozonishini bilganida, jiddiyroq kurashgan bo‘lar edi.

Sem LLoydning shaxsiy qaydnomalarida bu haqida shunday yozuvlar bor:

«Farosat olamining qadimiy ahllari, — deb yozadi Lloyd, — 70-yillar (XIX-asr nazarda tutilmoqda-tarjimon), boshida mening «15 o‘yini« nom bilan dong‘i ketgan surilma shashkali quticham ustida bosh qotirishga majbur etganligimni eslasalar kerak. o‘n beshta shashka kvadrat qutichaga to‘g‘ri tartibda terilgan bo‘lib, faqat 14- va 15-raqamli shashkalar o‘rni almashtirib qo‘yilgan. Vazifa — shashkalarni ketma-ket surish bilan 14- va 15-raqamli shashkalarning tartibini to‘g‘rilashdan iborat.

Shu masalani birinchi bo‘lib to‘g‘ri yechganga 1000 dollar mukofot va’da qilingan. Garchi uni yechish ustida hamma bosh qotirgan bo‘lsa-da, va’da qilingan mukofotga hech kim sazovor bo‘la olmadi. Odamlarning aytishlaricha qiziq-qiziq voqealar yuz bergan: savdogarlar do‘konlarini ochishni unutib qo‘yganlar; katta amaldorlar bu masalani yechish ilinjida kechalari ko‘cha fonuslari ostida o‘tirib tong ottirib chiqqanlar. Masalani yechimini izlashdan hech kim qaytmagan, chunki o‘yin bilan shug‘ullanuvchilarning barchasi muvaffaqiyat va mukofotdan umidvor edilar. Aytishlaricha o‘yinga qiziqib berilib ketgan shturmanlar kemalarni sayozliklarga o‘tirib qolishiga sababchi bo‘lishgan, mashinistlar poyezdlarni to‘xtatishni unutib,stansiyalardan o‘tib ketganlar, dehqonlar haydab turgan qo‘shlarini unutib, o‘yin bilan ovora bo‘lib qolganlar.

Quyida mazkur o‘yin nazariyasining boshlang‘ich qismi bilan tanishtirishga harakat qilib ko‘ramiz: bu nazariya to‘la holda juda murakkab va oliy matematika bo‘limlaridan biri («aniqlovchilar-determinantlar nazariyasi«ga) yondoshadi. Biz ba’zi qisqa mulohazalar bilan cheklanamiz.

o‘yinning vazifasi undagi bo‘sh joydan foydalanib, shashkalarni ketma-ket surish orqali 15-chi raqamli shashkani istalgan boshlang‘ich holatidan, me’yoriy holatga keltirishdan, ya’ni, sonlarni o‘z tartibida joylashtirishdan iboratdir; chunonchi: yuqoridagi chap burchakda 1, uning o‘ng tomonida 2, keyin 3, so‘ngra esa, yuqori o‘ng burchakda 4, undan pastki qatorda 5,6,7, va ho kazo. Shashkalarning bunday joylashuvi quyidagi 1-rasmda ko‘rsatilgan:

 

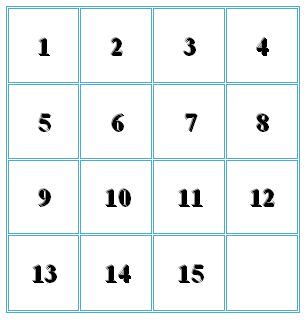
Endi 15-raqamli shashka tartibsiz joylashgan deb ko‘z oldingizga keltiring. Shashkalarni bir necha marta joyda-joyga surish bilan, 1-raqamli shashkani rasmda ko‘rsatilgan joyga keltirish mumkin.

Xuddi shuningdek, 1-shashkani joyidan qo‘zg‘atmay 2-shashkni uning o‘ng yoniga keltirib qo‘yish mumkin. so‘ngra 1-va 2-shashkalarni tegmasdan, 3- va 4-shashkalarni joyiga surib keltirib qo‘yish mumkin. mabodo ular keyingi vertikal qatorda bo‘lmasa, ularni o‘z o‘rniga keltirish uchun boshqa raqamli shashkalarni ketma-ket surib, istalgan natijaga erishish osonroq. Yuqori satr 1,2,3,4 tartibiga tushgach, ikkinchi satrni terishni boshlasa bo‘ladi. Bu satrni ham nisbatan osonlik bilan tartiblash hamma vaqt imkonlidir. Shundan so‘ng oxirgi ikki qator oralig‘ida 9 dan 13 gacha bo‘lgan shashkalarni terish kerak. Buni bajarish ham doimo imkonli bo‘lib, katta murakkablik tug‘dirmaydi. Tartibga solingan hamma shashkalardan (1-dan 13-gacha) birortasi ham endi o‘z joyidan qo‘zg‘almaydi; oltita katakdan iborat chog‘roq qism qoladi. Bunda bir katak bo‘sh, qolgan beshtasi, ixtiyoriy (tasodifiy) tartibda joylashgan 10, 11, 12, 14 va 15 raqamli shashkalar bilan band. Shu olti katakli joyda, 10, 11 va 12 raqamli shashkalarni doimiy me’yoriy tartibda terish mumkin. bunga erishilganidan keyin, oxirgi qatordagi 14- va 15-shashka yoki o‘z tartibida, yoki teskari tartibda joylashgan bo‘ladi.

Shu yo‘l bilan qiyidagi natijaga kelamiz.

Har qanday boshlang‘ich holat yoki 1- rasmdagi vaziyatga keltirilishi mumkin, yoki quyidagi 2-rasmdagi vaziyatga keltirilishi mumkin.

 

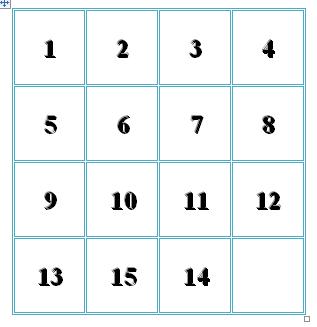
Agar biror vaziyat, (biz uni qisqalik uchun S harfi bilan belgilaymiz), 1-rasmdagi holatga keltirilishi mumkin bo‘lsa, u holda uning teskarisicha, ya’ni 1-rasmdagi holatni S holatga keltirish mumkin. shashkalarning hamma yurishlari teskarisiga qayta oladi; masalan: 1-sxemasa biz 12-raqamli shashkani bo‘sh katakka joylashtira olsak, shu yurishni darhol teskari harakatlar bilan qaytarish mumkin.

Shunday qilib biz ikki seriyali joylashishni ko‘ramiz. Bir seriyaning holatlari 1-rasmdagi kabi, ikkinchi seriyaniki esa, 2-rasmdagi kabi holatga keltirilishi mumkin. va aksincha, birinchi me’yoriy joylashishdan birinchi seriyaning istalgan holatini ikkinchi joylashishdan esa ikkinchi seriyaning istalgan holatini hosil qilish mumkin. nihoyat, bitta seriyaga tegishli istalgan ikkita ketma-ketlikni bir-biriga keltirish mumkin.

Yana ilgari siljish va shu birinchi va ikkinchi joylashishlarni birlashtirish mumkin bo‘lmasmikin? Bu holatlar har qancha yurish bilan ham biri ikkinchisiga aylanmasligini qat’iy isbot etish mumkin (lekin buning tafsiloti juda uzun bo‘lgani sababli, uni bayon qilib o‘tirmaymiz). Shuning uchun shashkalarning juda ko‘p sonda joylanish tartiblari, bir biriga aloqasi bo‘lmagan ikki xil turkumga ajraladi: 1) 1-rasmdagi kabi me’yoriy holatga keltirish mumkin bo‘lgan seriyalar turkumi; 2) 2-rasmdagi kabi holatga keltirish mumkin bo‘lgan seriyalar turkumi; demak, bularni hech qachon me’yoriy joylashish tartibiga keltirib bo‘lmaydi. Aynan shu ikkinchi seriyali turkumdagi istalgan holatni yechgan kishiga, juda ulkan qiymatlardagi mukofotlar tayinlanar edi.

Berilgan joylanish tartibini birinchi yoki ikkinchi turkumlardan qay biriga tegishli ekanini (ya’ni yechish mumkin yoki mumkin emasligini) qanday bilsa bo‘ladi? buni quyidagi misol ochib beradi:

Bunday joylanish tartibini qarab chiqaylik:

Birinchi qatordagi shashkalar tartibli, ikkinchi qatorda ham so‘nggi 9-raqamli shashkadan boshqa shashkalar hammasi o‘z tartibida. Demak, -raqamli shashka, 8-shashkaning o‘rnini egallab olgan. Ya’ni 9-shashka, 8-shashkadan ilgari turibdi: bu kabi joylanuv «tartibsizlik holati« deyiladi. 9-raqamli shashka haqidagi xulosa shu: bu joylanuvda bitta tartibsizlik bor. Endi keyingi shashkalarni ko‘zdan kechirsak: 14-shashkaning ham o‘zining joylashishi lozim bo‘lgan o‘rnidan ancha ilgari, oldinga qo‘yilganini ko‘ramiz. Bunda uchta tartibsizlik mavjud (14 raqamli shashka, 12, 13 va 11 dan oldinda turibdi). Demak tartibsizliklar soni 1+3=4 ta. So‘ngra, 12-shashka 11-shashkadan ilgari qo‘yilgan, xuddi shunga o‘xshab, 13-shashka ham 11-shashkadan oldinda turibdi. Bundan yana 2 ta tartibsizlik kelib chiqmoqda. Hammasi bo‘lib 6 ta tartibsizlik yuzaga kelganini ko‘ramiz. Har qanday joylanuv uchun tartibsizliklarning umumiy yig‘indisi shu tarzda aniqlanadi. Lekin, so‘nggi pastki qatorning o‘ng tomondagi oxirgi o‘rni doim bo‘shatib qo‘yiladi. Agar, tartibsizliklarning umumiy soni, hozir ko‘rib o‘tganimizdek juft sonda bo‘lsa, u holda berilgan istalgan joylanuvdagi variantni me’yori tartibga keltirish mumkin; boshqacha aytganda u yechiladigan masalalar turkumiga kiradi. Bordiyu, tartibsizliklar soni toq bo‘lsa, bunday joylanish ikkinchi turkumga, ya’ni, yechib bo‘lmaydigan masalalar turkumiga mansub bo‘ladi. (nol tartibsizlik jut tartibsizlik deb qabul qilinadi).

Bu o‘yinning mohiyatini matematika ochib berganidan so‘ng, unga bo‘lgan ommaviy ishqibozlik ilgarilaridek bo‘lmay qoldi. Sababi, o‘yinga bo‘lgan qiziqishning yarmidan ko‘p behuda urinishlarga sarflanadigan masalalar ustida ekanligi ma’lum bo‘lib qoldi. Matematika, bu o‘yinning mukammal nazariyasini, hech qanday shubha qoldirmaydigan darajada bayon qilib berdi. o‘yinning oqibat natijasi, boshqa ayrim o‘yinlardagi kabi, biror tasodif, yoki o‘yinchining ziyrakligiga emas, balki shu natijaning so‘zsiz to‘g‘ri chiqishini oldindan belgilab beruvchi matematika faktorlargagina bog‘liqdir.

 

Endi shu sohaga oid jumboqlarga murojaat qilamiz.

Quyida o‘yin ixtirochisi Sem LLoydning o‘zi o‘ylab topgan, yechiladigan masalalardan uchtasini havola qilamiz.

1. LLoydning birinchi masalasi.

1-rasmda ko‘rsatilgan joylashuv tartibini boshlang‘ich holat deb olib, shashkalar to‘g‘ri tartibga keltirilsin, ammo yuqori chap burchakdagi katak bo‘sh qoldirilsin (3-rasm)

 

.

1. LLoydning ikkinchi masalasi.

1-rasmdagi joylanish tartibini boshlang‘ich holat deb olib, qutichani soat strelkasi yo‘nalishida chorak aylanish o‘ngga buring va shashkalar 4-rsamdagi kabi tartibni olmagunicha ularni joydan joyga surishni davom ettiring.

 

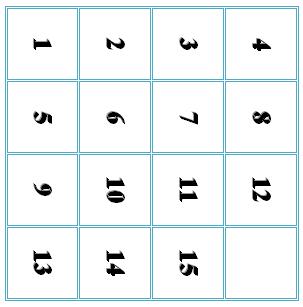
1. LLoydning uchinchi masalasi.

1-rsamdagi joylanishga asoslanib, shashkalarni «sehrli kvadrat» tartibida yig‘ing. Ya’ni, ularni shunday joylashtiringki, sonlarning har qanday yo‘nalishdagi yig‘indisi 30 ga teng bo‘lsin.

 

Masalalarning javoblari.

---