Neyl yarim kubik parabolasining yoy uzunligi

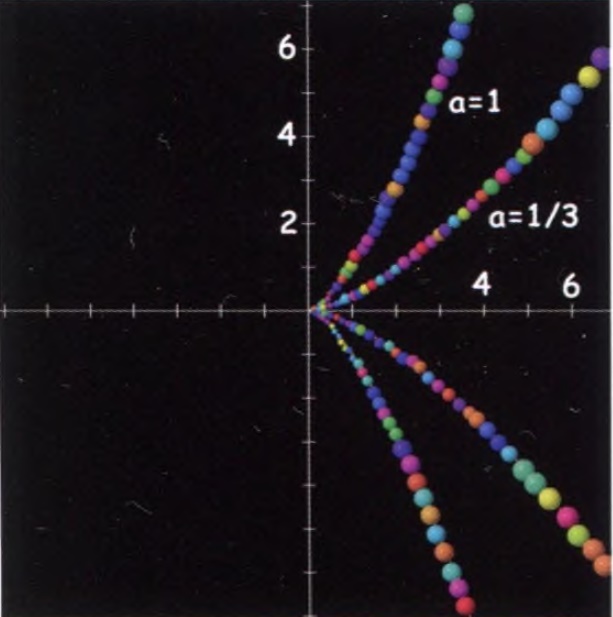Matematika tarixida notrivial algebraik egri chiziqning yoy uzunligini aniqlagan ilk olim Angliyalik Uilyam Neyl (1637-1670) bo‘ladi. Uilyam Neyl 1657-yilda yarim kubik parabola deb nomlanadigan va y²=ax³ tenglama orqali ifodalanadigan egri chiziq uchun yoy uzunligini hisoblashning uddasidan chiqdi. Agar tenglamani y=±bx^3/2 tarzida shakl almashtirishga keltirilsa, nima sababdan egri chiziqni yarim kubik deb nomlanishi oydinlashadi va «kubning yarmi« masalaga qayerdan aralashib qolayotganini payqash mumkin bo‘ladi. Neylning ushbu yo‘nalishda qayd etgan natijalari haqida yana bir yetuk matematik — Jon Vallis (1616-1703) tomonidan 1659-yilda e’lon qilingan «Sikloida haqida» nomli asarda alohida to‘xtalib o‘tilgan va butun dunyo ilmiy jamoatchiligiga ma’lumot yetkazilgan. Qizig‘i shundaki, Neylning mazkur ishigacha matematikada faqat logarifmik spiral va sikloida singari transendent egri chiziqlarning yoy uzunligini aniqlashga muvaffaq bo‘lingan xolos edi.

Giperbola va ellips singari egri chiziqlarni yoy uzunligini hisoblashga bo‘lgan ko‘plab urinishlar bekor ketganligi sababli, o‘sha zamonlardagi eng yetuk matematiklar, shu jumladan Rene Dekart (1569-1650) ham egri chiziqlarning hammasini ham yoy uzunligini hisoblab bo‘lmaydi, juda kam sonli, ayrim turdagi egri chiziqlarnigina yoyini hisoblash mumkin degan uzil-kesil xulosaga kelib qolishgan edi. Biroq, bunday fikrning noto‘g‘ri va noo‘rin ekanligini tez orada italyan olimi Evanjelista Torichelli (1608-1647) isbotlab berdi. Logarifmik spiralning yoy uzunligini hisoblash yo‘lini birinchi bo‘lib aynan Torichelli ishlab chiqqan edi. Asosan Galileyning shogirdi ekani va atmosfera bosimining mavjud ekanini isbotlab berganligi bilan ko‘proq mashhur bo‘lgan Torichellining logarifmik spiral yoy uzunligini hisoblashni uddasidan chiqishi bilan, ushbu egri chiziq yoy uzunligi va umuman egri chiziq uzunligini matematik hisoblash imkoni paydo bo‘lgan ikkinchi egri chiziqqa aylandi. Bundan avval geometriya olamida faqat aylana to‘liq uzunligini va yoy uzunligini aniqlash mumkin edi xolos. Aylana va logarifmik spiraldan keyingi, uzunligini matematik hisoblash orqali aniqlash imkoni ochilgan uchinchi egri chiziq bu — sikloida bo‘lgan. Sikloida uzunligini hisoblash usulini 1658-yilda Angliyalik mashhur me’mor va shu sababli kasbi yuzasidan geometriyani ham mukammal bilgan shaxs — Kristofer Ren (1632-1723) ochib bergan.

1687-yillar atrofida yana bir buyuk fizik va matematik olim, Xristian Gyuygens (1629-1695) yarim kubik parabola bu — gravitatsiya ta’sirida qulayotgan jismning vaqt birligi ichida pastga tomon bosib o‘tadigan yo‘li bo‘lib, u ushbu vaqtga teng vaqt ichida mazkur jismning vertikal yo‘nalishda bosib o‘tgan yo‘liga teng ekanini isbotlab berdi. Yarim kubik parabolani shuningdek x=t² va y=at³ tenglamalar sistemasi orqali ham ifodalash mumkin. Bunday shaklda qaralganda, egri chiziqning uzunligi t ning funksiyasi sifatida olinadi va

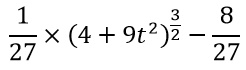
ni tashkil qiladi. Boshqacha aytganda, egri chiziqning uzunligi 0 dan t gacha bo‘lgan intervalda bo‘ladi. Ilmiy adabiyotlarda Neyl parabolasi uchun asosan y²=ax³ tenglama keltiriladi.

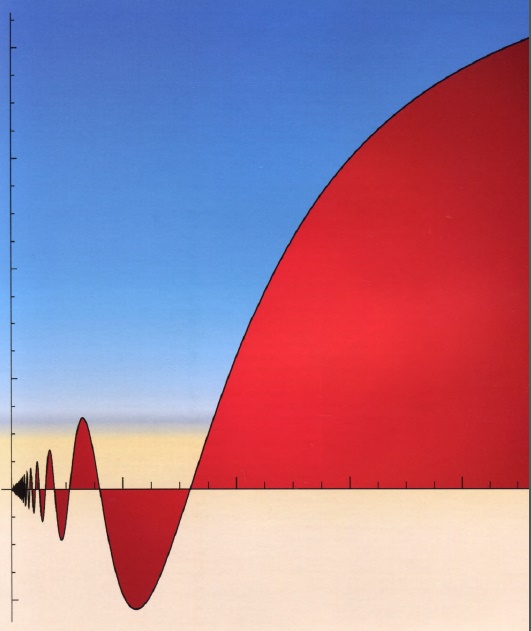
Ba’zi egri chiziqlarning uzunligini hisoblashning imkon yo‘q, ya’ni, bunday egri chiziqlar cheksiz uzunlikka ega bo‘ladi. Ushbu grafik f(x)=x·sin(1/x) funksiyaning 0xx=0 va f(0)=0 nuqta bilan chegaralangan bo‘ladi va istalgan ochiq to‘plam uchun cheksiz uzunlikka ega bo‘ladi.