Kepler qonunlari

1: Sayyoralar Quyosh atrofida cho‘zinchoq elliptik orbitalar bo‘yicha harakatlanadi, ushbu ellips fokuslaridan birida Quyosh joylashgan bo‘ladi.

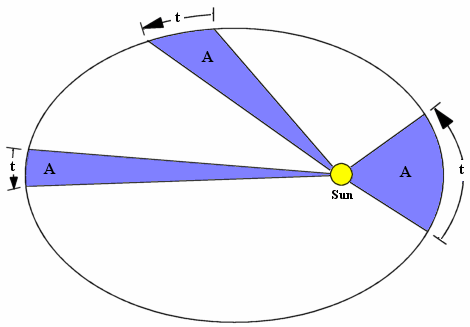
2: Quyosh va sayyorani tutashtiruvchi xayoliy to‘g‘ri chiziq, teng vaqtlar orasida ellipsni teng yuzalarga taqsimlaydi.

3: Sayyoralarning Quyosh atrofida aylanib chiqish davrining kvadratlari nisbati, ushbu sayyora orbitasi katta yarim o‘qlari nisbatiga teng bo‘ladi.

 

Iogann Kepler ajoyib ichki hissiy anglash, intuitsiya egasi bo‘lgan. U butun umri davomida, Quyosh sistemasining qandaydir ajoyib sirli san’at asari ekanligini isbotlashga tirishgan. Avvaliga u Quyosh sistemasi tuzilishini qadimgi yunon geometriyasidan buyon saqlanib kelayotgan besh xil to‘g‘ri ko‘pyoqlar bilan bog‘lab izohlashga urindi. (To‘g‘ri ko‘pyoqlar bu – barcha yoqlari teng yonli muntazam ko‘pburchaklardan iborat bo‘lgan uch o‘lchamli jism bo‘ladi). Kepler zamonasida astronomlar faqat oltita sayyorani bilishar edi va tasavvurga ko‘ra ular, «shaffof sferalar» ichida joylashib harakatlanadi deb qaralardi. Kepler o‘z ilmiy kuzatish va tekshirishlarini, ushbu sferalarning o‘zaro joylashuvi bir-birining ichiga ichki chizilgan (to‘g‘rirog‘i, ichki joylashgan) to‘g‘ri ko‘pyoqlar ko‘rinishida bo‘ladi degan fikrni tekshirib ko‘rishdan boshlagan. Uning tasavvuriga ko‘ra: Saturn va Yupiter orasida kub, Yupiter va Mars orasida esa tetraedr, Mars va Yer orasida dodakaedr, Yer va Venera orasida ikosaedr, Venera va Merkuriy orasida oktaedr tartibdagi sferalar joylashadi deb o‘ylagan. Ma’lumingizkim, to‘g‘ri ko‘pyoqlari (ularni shuningdek, «Platon jismlari» ham deyiladi) 5 xil va o‘sha zamonda odamlarga ma’lum bo‘lgan sayyoralar esa 6 ta edi. Shunga muvofiq, Kepler har bir sayyora orasida shunday to‘g‘ri ko‘pyoqlardan birortasi ko‘rinishidagi shaffof sfera mavjud bo‘lsa, bu osmon jismlari harakati mukammallik, ideallik bo‘ladi deb o‘ylagan. U hayotining bu qismida, sayyoralar harakati va umuman Koinot albatta ideal bo‘lishi kerak degan fikrda edi.

 

 

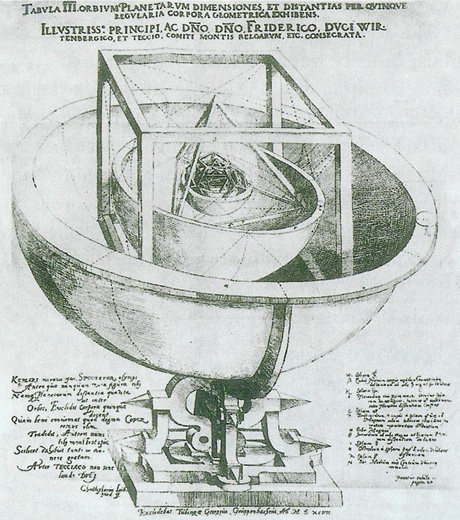Biroq, xayolot va tasavvurdagi ideallik bilan amaldagi, real voqe’lik deyarli hech qachon o‘zaro mos tushmaydi. Keplerning xayoloti bo‘lgan to‘g‘ri ko‘pyoqlar ko‘rinishidagi shaffof sferalarda harakatlanadigan sayyoralar orbitasi haqidagi tasavvuri, olimning sayyoralarni real hayotda, o‘zi ko‘zi bilan yaqqol ko‘rib kuzatib turgan holatdagi harakat orbitasi bilan mutlaqo mos tushmasdi. Bu haqida olimlardan biri quyidagicha ta’rif bergandi: «Kepler tasavvuridagi mukammal, go‘zal manzara, real hayotdagi badbashara faktlar bilan buzib tashlangan…». Kepler u paytlar yosh edi va uning o‘sha paytdagi ilmiy tasavvurlarining xotirasi o‘laroq, u o‘z qo‘llari bilan yasagan va gersog Frederik fon Vyurtemburgga sovg‘a qilgan Quyosh sistemasi modeli saqlanib qolgan. Ushbu, qunt bilan ishlangan metall konstruksiyada yosh Kepler sayyoralarni aynan Platon jismlaridan iborat sferalar ichida joylashgan tarzda ifodalagan. Kepler yasagan ushbu modeldagi sferalar bir-biriga tutashmagan ichi bo‘sh hajmlar bo‘lgan va ularning har birining ichiga turli ichimliklar quyish mumkin bo‘lgan. Gersog turli ziyofatlar paytida «Osmon modeli»dan quyilgan ichimliklar bilan o‘z mehmonlariga iltifot ko‘rsatgan.

Kepler Praga shahriga, o‘sha zamonning eng yetuk astronomi Tixo Brage (1546-1601) oldiga shogird bo‘lib borgachgina, sayyoralar harakati mexanizmlaridan qandaydir mukammallik izlash o‘rniga, real kuzatishlar asosida, haqiqiy orbitalarni o‘rganish kerakligini angladi. Tixo Brage butun hayoti davomida astronomik kuzatishlar olib borgan va sayyoralarning harakati borasida juda katta ma’lumot to‘plagan edi. Brage vafot etgach, uning barcha qo‘lyozmalari, hisob-kitoblari va chizmalari Kepler ixtiyorida qolgan. O‘sha paytlarda Bragening mazkur merosi juda katta tijoriy qiymatga ega edi. Chunki, ular asosida, o‘sha paytlarda munajjimlar turli astrologik bashoratlar ishlab chiqib pullashgan (ko‘pchilik odamlar u zamonlar shunday bashoratlarga ishonishar edi, nima ham derdik, munajjimlar «bashoratiga» laqqa tushadigan soddalar hozir ham bor). Shunga qaramay, o‘zi muttasil pulga muhtoj bo‘lsa-da, Kepler ustozining yozuv-chizuvlarini sotmadi va aksincha, ular asosida, yanada mukammal kuzatishlar va tahlillar o‘tkazishga kirishdi.

Tixo Bragening kuzatishlari natijalarini tahlil qilish asnosida Kepler hatto zamonaviy kompyuterlar yordami bilan ham hisob-kitob qilishga qiyinlik qiladigan masalalarni yechishiga to‘g‘ri kelgan. Biroq, unda tanlov imkoniyati bo‘lmagan va barcha zamondoshlari kabi, u ham hamma algebraik hisoblashlarni qo‘lda bajarishiga to‘g‘ri kelgan. Albatta, o‘z davrining ko‘plab astronomlari singari, Kepler ham Kopernikning geliosentrik nazariyasi bilan yaxshi tanish edi va Yer Quyosh atrofida aylanishini tushunardi. Lekin, Yer va boshqa sayyoralar Quyosh atrofida aynan qanday aylanadi? – degan savol uni qiynardi. Tasavvur qiling, siz, birinchidan, o‘z o‘qi atrofida aylanadigan, ikkinchidan, Quyosh atrofida o‘zingizga noma’lum orbita bo‘ylab harakatlanadigan sayyora sirtidasiz. Osmonni kuzatib, siz bizga noma’lum o‘z orbitasi bo‘ylab harakatlanadigan boshqa sayyoralarni ham ko‘rasiz. Vazifangiz esa, o‘zi ham muttasil harakat va aylanishda bo‘lgan sayyoradan turib kuzatish orqali, o‘z sayyorangiz va boshqa sayyoralarning ham orbita geometriyasini va harakat tezligini aniqlashdan iborat. Kepler aynan shu ishni uddalagan va yakunda, kuzatish natijalari orqali o‘zining o‘sha mashhur uchta qonunini keltirib chiqargan!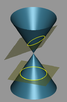

Keplerning birinchi qonuni sayyoralarning orbitalari geometriyasining trayektoriyasini bayon qilib beradi. Siz maktab geometriya kursini yodga olsangiz, ellips degan shakl esingizga tushsa kerak. Ellips – tekislikda har bir nuqtasidan fokuslar deb ataluvchi berilgan ikki F_1, F_2 nuqtagacha bo‘lgan masofalari yig‘indisi berilgan PQ kesma uzunligiga teng bo‘lgan barcha nuqtalar to‘plamiga aytiladi. Berilgan kesma uzunligi fokuslar orasidagi masofadan katta.. Agar bu ta’rif qiyinlik qilgan bo‘lsa, unda ellipsni konus kesimlaridan biri ko‘rinishida ham tasavvur qilish mumkin. Bunda, konusni uning asosiga va yoniga parallel bo‘lmagan (asosiga nisbatan muayyan burchak) tekislik kesib o‘tsa, aynan ellips hosil bo‘ladi (rasmda).  Keplerning birinchi qonuni, sayyoralarning orbitasi aynan ellips shaklida ekanini ta’kidlaydi va uning fokuslaridan birida Quyosh joylashadi deb uqtiradi. Barcha sayyoralarning orbitalari ekssentrisiteti (cho‘zinchoqligi) va ularning perigeliy va apogeydagi[1] Quyoshgacha bo‘lgan masofasi turlichadir. Biroq, barcha elliptik orbitalar uchun umumiy bo‘lgan yagona jihat bor: ularning barchasida fokuslarining birida albatta Quyosh joylashgan bo‘ladi. Tixo Bragening kuzatish natijalarini o‘rganib chiqib, Kepler sayyoralarning elliptik orbitalari bir-biri bilan ustma-ust tushadigan ellipslardan iborat ekanini fahmlab qoldi. Bu astronomiya tarixida shu choqqacha hali hech kimning kallasiga kelmagan kashfiyot edi.

Keplerning birinchi qonunining tarixiy ahamiyatiga munosib asl bahosini berish qiyin. Ungacha bo‘lgan astronomlarning deyarli barchasi sayyoralar ideal aylana shaklidagi orbitalar bo‘ylab harakatlanadi deb qarashgan. Agar kuzatishlar bunga muvofiq kelmasa, asosiy aylana harakat orbitasiga qo‘shimcha qilib, yana kichik aylana orbitalari degan tushunchani kiritishgan. Shunchaki, ular sayyora orbitasi albatta aylana shaklida bo‘ladi degan fikrni rost bo‘lib chiqishini shu darajada istashar ediki, o‘zlari uchun o‘zlari shunday tuzatishlar kiritib olishar edi. Ta’bir joiz bo‘lsa, bunday tushuncha Kepler davrigacha bo‘lgan astronomlarga ham asrlar osha yetib kelgan falsafiy qarashlar mahsuli bo‘lib, ular osmon jismlari va umuman Koinot mukammal tuzilgan deb ishonishgan. Ularning nazdidagi mukammallik, komillik timsoli esa aylana va shar shaklidagi sfera bo‘lgan. Shu sababli, o‘sha zamonlarda faylasuflar, sayyoralar albatta aylana bo‘ylab harakatlanadi degan aqidaga qattiq yopishib olishgan edi. Umuman olganda, hozir ham ba’zan shunday yanglish tushunchani odamlar fikridan ketkazishga to‘g‘ri keladi. Kepler esa, ustozining qo‘lyozmalaridagi ma’lumotlar orqali, odamlar va hatto olimlar ongida ham o‘rnashib, ildiz otib ketgan ushbu yanglish tushunchani barbod qildi. Xuddi, Kopernik geosentrik olam markazidan Yerni «quvib solgani» va geliosentrik nazariyani barpo qilgani kabi, Kepler ham sayyoralar orbitasi geometriyasi bilan bog‘liq shunday g‘aliz qarashlarni, reallikka to‘g‘ri kelmaydigan, xayolotga asoslangan ziddiyatlarni quvib chiqarishga muvaffaq bo‘ldi.

Keplerning ikkinchi qonuni sayyoraning Quyosh atrofidagi harakat tezligi haqida so‘z yuritadi. Unga ko‘ra, sayyora Quyoshga qancha yaqin kelsa, uning tezligi shunga monand ortadi; elliptik orbita bo‘ylab u Quyoshdan qancha olis ketsa, tezligi ham shunga mos ravishda pasayadi. Bunda, teng vaqt intervallari bo‘yicha, sayyora va Quyoshni tutashtirib turuvchi xayoliy chiziq bilan chegaralangan ellips sektorlarining yuzasi doimo teng bo‘ladi.

Ushbu ikki qonunni yaxshi bilgan holda, istalgan sayyoraning orbitasini aniq hisoblash va istalgan vaqt uchun uning osmonning qayerida joylashishini bilish mumkin. Birinchi va ikkinchi qonunlarda, alohida bir sayyora uchun orbital trayektoriyaning o‘ziga xosliklari haqida gap boradi.

Keplerning uchinchi qonuni esa sayyoralarning orbitalarini o‘zaro taqqoslash imkonini beradi. Unga ko‘ra, sayyora Quyoshdan qanchalik olisda joylashgan bo‘lsa, uning Quyosh atrofini to‘liq aylanib chiqishi uchun ketadigan vaqti ham shunga monand uzoqroq muddatni egallaydi deyiladi. Ya’ni, sayyora Quyoshdan qancha uzoq bo‘lsa, undagi yil davomiyligi ham shuncha uzun bo‘ladi. Hozirda biz yaxshi bilamizki, bu holat ikki omilga ko‘ra yuzaga keladi. Birinchidan, olisda joylashganlik faktining o‘zi, uning orbitasi perimetrining ham katta bo‘lishini taqozo etadi va demakki, o‘z-o‘zidan, sayyora ko‘proq yo‘l bosib o‘tishiga to‘g‘ri keladi; ikkinchidan, Quyosh bilan oraliq masofaning kattaligi tufayli, sayyoraning orbita bo‘ylab chiziqli harakat tezligi ham pasayadi. Oqibatda, u olis yo‘lda sekin harakatlanadigan bo‘ladi. Umuman olganda, Keplerning uchinchi qonuni ta’rifi quyidagicha yangraydi: istalgan sayyoraning Quyosh atrofini aylanib chiqish davrining kvadrati, uning elliptik orbitasining katta yarim o‘qi masofasining kubiga proporsional bo‘ladi.

Aytish joizki, Kepler o‘z qonunlarini keltirib chiqarishda, shunchaki faktlarni qayd qilishga asoslangan va kuzatuv natijalarini umumlashtirgan xolos. Ya’ni, u mazkur qonunlarni keltirib chiqarishda qandaydir bir nazariy tayyorgarlik va isbotlashlarga suyanmagan. Masalan, siz undan nima uchun ikkinchi qonunda sayyoraning teng vaqt oraliqlarida kesib o‘tgan sektorlari yuzasi ham o‘zaro teng bo‘ladi? – deb so‘rasangiz, savolingizga ilmiy javob ololmagan bo‘lardingiz. Chunki, u shunchaki, bu amalda shunday ekanini kuzatishlar orqali aniqlagan (ya’ni, empirik keltirib chiqargan) xolos. Ya’ni, u o‘tkazgan tahlillar shunday natija bergan, vassalom! Agar siz undan boshqa yulduz sistemalaridagi sayyoralarning orbitasi qanday bo‘ladi deb so‘rasangiz, u yana hammasini boshidan boshlab, bir necha yillik kuzatishlar o‘tkazib, natijalarni tahlil qilib chiqishiga to‘g‘ri kelar edi. Keyin esa, ushbu tahlillar asosida qandaydir qonuniyatni topsa, sizga javob aytgan bo‘lardi. Ya’ni, u boshqa yulduz sistemasidagi sayyoralar harakati ham, Quyosh sistemasidagi sayyoralar bo‘ysunadigan qonunlarga bo‘ysunishi haqida tasavvurning o‘zi bo‘lmagan.

Nyuton mumtoz mexanikasining eng buyuk yutuqlaridan biri ham aynan shunda. Ya’ni, Nyuton, Kepler qonunlarining fundamental asoslarini ochib beradi va ularning istalgan sistemaga tadbiq qilinishi mumkinligini, ya’ni, universial ekanligini ta’kidlaydi. Oxir-oqibat shunday bo‘lib chiqdiki, Kepler qonunlarini Nyuton qonunlaridan matematik yo‘l bilan keltirib chiqarish mumkin ekan! Basharti shunday ekan, demak biz, Kepler qonunlari Koinotdagi istalgan sayyoralar sistemasi uchun yaroqli ekaniga ishonch hosil qilishimiz mumkin. Astronomlar haqiqatan ham, hozirda ketma-ket ochilayotgan ekzosayyoralar sistemalari uchun ushbu qonunlarni tadbiq etishmoqda va ular haqiqatan ham, katta aniqlik bilan o‘zini oqlamoqda! (Aytgancha, kashf etilayotgan ekzosayyoralar nomiga ham Keplerning nomi qo‘shib aytilishi urfga kirdi. Buning sababi, u kashf qilgan mazkur qonunlar bilan emas, baliki, o‘sha ekzosayyoralarning kashf etilishi uchun vosita-sababchi bo‘lgan «Kepler» teleskopi tufaylidir. Masalan, K2-18b ekzosayyorasi «Kepler» teleskopining ikkinchi missiyasi davomida kashf qilingan).

Keplerning ushbu uchinchi qonuni zamonaviy kosmologiya fanida ham juda katta ahamiyat kasb etadi. Chunonchi, olis galaktikalarni kuzatish asnosida, astrofiziklar, galaktika markazlaridagi vodorod atomlaridan chiqadigan kuchsiz signallarni qayd etishadi. Ushbu nurlanishlar spektridagi Doppler effekti bo‘yicha olimlar galaktika diskining vodorod periferiyasining aylanish tezligini aniqlashadi va bu orqali, galaktikalarning o‘zining burchak tezliklarini topishadi.

Kepler qonunlari tabiat va borliqni anglashda insoniyat tushunib yetgan eng birinchi va eng muhim qonunlardan biridir. O‘zida fizika, matematika va astronomiyani uyg‘unlashtirgan holda, Kepler qonunlari ilm-fanda, tabiat hodisalarini ixcham va oddiy formulalar bilan ifodalash mumkinligini ham ko‘rsatib berdi va minglab keyingi avlod olimlari uchun namuna o‘laroq xizmat qildi.

---

[1] Perigeliy – sayyoraning Quyoshga eng yaqin keladigan nuqtasi, apogey esa Quyoshdan eng uzoq ketadigan nuqtasi nomi

 

 

---