Silashi ko‘pyog‘i

Ko‘pyoq deb, yoqlari tekisliklardan va qirralari to‘g‘ri chiziqdan iborat bo‘lgan uch o‘lchovli jismlarni aytiladi. Kub, to‘g‘ri tetraedr singari ko‘pyoqlarni deyarli hamma yaxshi taniydi. To‘g‘ri tetraedr bu — teng yonli uchburchaklardan yasalgan to‘rt tomonli piramidadir. Ko‘pyoqni «to‘g‘ri ko‘pyoq» deb atash uchun, ushbu ko‘pyoqning hamma yoqlari teng bo‘lishi kerak.

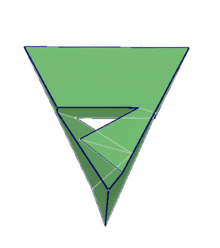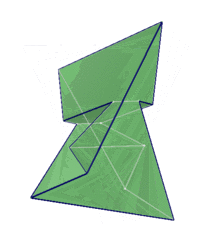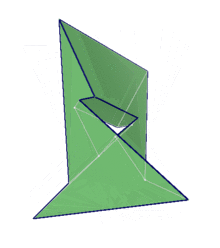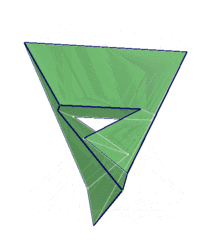
Silashi ko‘pyog‘ini 1977-yilda vengr matematigi Layosh Silashi tomonidan aniqlangan. Silashi ko‘pyog‘i geometriyada geptaedr, ya’ni, yettiyoq deb yuritiladi (ya’ni, uning yettita yoqlari mavjud). Yetti yoqlarning har biri oltiburchaklardan iborat bo‘lib, 21 ta qirra va 14 uchga va bitta tirqishga ega. Silashi ko‘pyog‘i 180° lik simmetriyaga ega. Yoqlarning uch jufti o‘zaro kongruentdir. Ya’ni, ular bir xil o‘lcham va shaklga egadirlar. Qolgan yoqlar esa o‘zaro simmetrik oltiburchaklardan iborat.

Eng qizig‘i shundaki, shu paytgacha geometriyada ma’lum ko‘pyoqlar ichida tetraedrdan tashqari faqat Silashi ko‘pyog‘igina har bir yoq boshqa yoqlarning har biri bilan umumiy qirraga ega bo‘ladi. Silashi ushbu ko‘pyoqni maxsus kompyuter dasturi orqali hisoblab chiqqan bo‘lib, mashhur matematik va fan targ‘ibotchisi Martin Gardnerning yozishicha, Silashi ushbu ko‘pyoqni aniqlamagunicha, matematiklar bunday strukturaning mavjudligi haqida o‘ylab ham ko‘rishmagan ekan.

Silashi ko‘pyog‘i shuningdek xaritalarni bo‘yash haqidagi masalaga ham oydinlik kiritdi. An’anaga ko‘ra, xaritadagi qo‘shni hududlarning rangi bir xil bo‘lib qolmasligi uchun, xarita eng kamida to‘rt xil rang bilan bo‘yalishi kerak. Silashi ko‘pyog‘i ustiga chiziladigan xarita uchun shunday ranglar turi yetti xil bo‘lishi lozim. Ya’ni, Silashi ko‘pyog‘ining ikki xil yog‘i bir xil rangda bo‘lib qolmasligi uchun, uning hamma yoqlari har xil rangda bo‘lishi shart. Taqqoslash uchun, tetraedr sirtiga xarita chizilsa, uning yoqlari bir xil rangda bo‘lib qolmasligi uchun, to‘rt xil rangning o‘zi yetarli bo‘ladi. Bu esa sfera uchun olinadigan rang turlari bilan topologik ekvivalentdir. Ushbu ikki ko‘pyoqlarning xossalari haqida quyidagicha qisqacha xulosa berish mumkin:

Tetraedr 4 yoqqa; 4 uchga; 6 qirraga; 0 ta tirqishga ega.

Silashi ko‘pyog‘i 7 yoqqa; 14 uchga; 21 qirraga; 1 ta tirqishga ega.